2. 交通整理 (2020/4/12)
佐藤氏のモデル 都道府県ごとのシミュ レーションによる検討について、 本堂毅氏、 佐野雅己氏、 松下 貢氏の連名による 批判が公開されています。
批判は4点で
- モデルが人口保存を満たしていない
- 時間遅れの扱いが標準的なものと違う
- モデルの検証がなされていない
-
予測に「最悪条件」を使うのは適切ではない
これは満たしていないことは間違いなく、既に
1.3 節で議論した通りです。これは、
佐藤氏のモデルでは、潜伏期にある人口が明示的に現れないからです。
S, I, R の他に「潜伏期にある人」が存在するのですから、これをいれないと
元の総人口にはならないのは明らかでしょう。
1.3 節の記法でいうと、
なので、
まあその、佐藤氏は
出版された論文でもこの式を使っているので、なかなか難しい問題がある気もします。
佐野氏らの批判では、佐藤氏の文章について
「時間遅れの入れ方に誤解があり、物理的にも意味がないモデルになっている
と思われます」
としています。その根拠は
「過去の多くの文献で
過去の文献と違うから間違っているに決まっている、というのは批判と
してちょっとどうかと思います。
文献が示されていないので過去の論文で実際にどういう扱いがされていたかわ
からないのですが、おそらくやはり「潜伏期の人口」を明示的にもたないもの
と思われます。具体的には
人口保存はするのですが、佐藤氏の方程式系に比べて解釈ははっきりしないものの
ように思います。佐藤氏が指摘しているように、違う時刻の変数が相互作用す
るのは厳密には意味をなさず、あくまでも近似的なものではないかと思います。
もう少し細かくいうと、この方程式系での x は潜伏期にある人を含むので、
これを x+e と置き直して、この式での
なので、
過去の文献と違うから間違いと決めつけるのは問題であり、過去の多くの文献
が近似的な扱いであったのではないかと思います。
これはまあ、十分とはいいがたいと思います。特に、モデルパラメータのうち
β、つまり回復する割合は都市毎にフィッテイングパラメータにする、という
のは、都市毎に病気が違うのでなければあんまり正当化できないですし、それ
なら時間遅れτは定数なのか?というのは疑問です。また、τを「潜伏期間+
症状が発見されるまでの時間差」としていますが、これはモデルの解釈として
は問題で、モデル変数としてはτは潜伏期間でなければならず、症状が発見さ
れるまでの時間差は別の形で与えなければパラメータ推定に失敗します。τの
過大評価は既に議論したように
2.1. モデルが人口保存を満たしていないこと
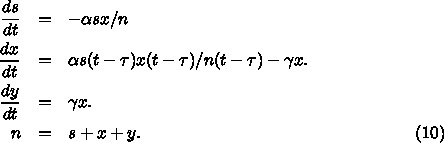
 前の sの減る分で、時刻が違う以上この2つは違うの
で、 s+x+y は変化して、その変化はもちろん、「潜伏期にある人」の変化で
あるわけです。
前の sの減る分で、時刻が違う以上この2つは違うの
で、 s+x+y は変化して、その変化はもちろん、「潜伏期にある人」の変化で
あるわけです。
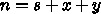 と定義するなら、それは潜伏期にある人を除外し
た人口であり、保存しなくてもかまわないので、方程式系が人口保存を満たし
ていないようにみえることはそれだけでは方程式系がおかしいということを
意味しません。しかし、
と定義するなら、それは潜伏期にある人を除外し
た人口であり、保存しなくてもかまわないので、方程式系が人口保存を満たし
ていないようにみえることはそれだけでは方程式系がおかしいということを
意味しません。しかし、
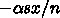 という形で係数の規格化に n が使われるのは若干問題
で、方程式系の意味を考えるとこれはちゃんと変化しない全人口でなければな
りません。
例えば、 x, y が小さいとして、それらが同じままで s を減らしてその分を「潜伏期にある人」にもっ
ていくと、上の式では
という形で係数の規格化に n が使われるのは若干問題
で、方程式系の意味を考えるとこれはちゃんと変化しない全人口でなければな
りません。
例えば、 x, y が小さいとして、それらが同じままで s を減らしてその分を「潜伏期にある人」にもっ
ていくと、上の式では
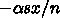 が s n の変化がうちけしあうのでほとんど変わらなくなるのですが、
本来は s が減ったことで小さくならなければなりません。
が s n の変化がうちけしあうのでほとんど変わらなくなるのですが、
本来は s が減ったことで小さくならなければなりません。
2.2. 時間遅れの扱いが標準的なものと違うこと
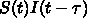 を使っているが
佐藤氏は
を使っているが
佐藤氏は 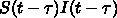 を使っている」というものです。
を使っている」というものです。
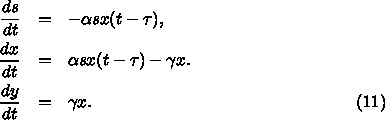
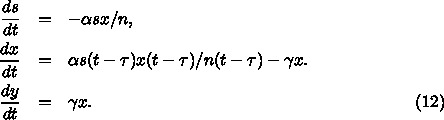
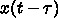 を x にして書き直すと、
私のだした式とは
を x にして書き直すと、
私のだした式とは 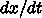 の項に
の項に 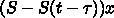 の差がでてきて、
そういう近似をしているわけです。
の差がでてきて、
そういう近似をしているわけです。
2.3. モデルの検証がなされていない
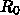 の過大評価に直結するので、あまり
安全とはいいがたいです。
の過大評価に直結するので、あまり
安全とはいいがたいです。
2.4. 予測に「最悪条件」を使うのは適切ではない