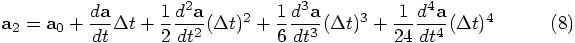A Fourth-Order Integrator
Coefficients
Bob: Now it is really time to show off my fourth-order integrator.
Alice: Can you show me again the code?
Bob: Here it is:
def rk4(dt)
old_pos = pos
a0 = acc
@pos = old_pos + vel*0.5*dt + a0*0.125*dt*dt
a1 = acc
@pos = old_pos + vel*dt + a1*0.5*dt*dt
a2 = acc
@pos = old_pos + vel*dt + (a0+a1*2)*(1/6.0)*dt*dt
@vel = vel + (a0+a1*4+a2)*(1/6.0)*dt
end
Alice: That’s quite a bit more complicated. I see coefficients of 1/6 and 1/3 and 2/3. How did you determine those?
Bob: I just looked them up from a book. There are several ways to choose those coefficients. Runge-Kutta formulas form a whole family, and the higher the order, the more choices there are for the coefficients. In addition, there are some extra simplifications that can be made in the case of a second order differential equation where there is no dependence on the first derivative.
Alice: As in the case of Newton’s equation of motion, where the acceleration is dependent on the position, but not on the velocity.
Bob: Exactly. Here are the equations. They can be found in that famous compendium of equations and tables and graphs: Handbook of Mathematical Functions, by M. Abramowitz and I. A. Stegun, eds. [Dover, 1965]. You can even find the pages on the web now. Here is what I copied from a web page:

Alice: Quite a bit more complex than the second order one.
Bob: Yes, and of course it is written in a rather different form that the way I chose to implement it. I preferred to stay close to the same style in which I had written the leapfrog and second-order Runge Kutta. This means that I first had to rewrite the Abramowitz and Stegun expression.
Really Fourth Order?
Alice: Let’s write it out specifically, just to check what you did. I know from experience how easy it is to make a mistake in these kinds of transformations.
Bob: So do I! Okay, the book starts with the differential equation:

whereas we want to apply it to Newton’s equation, which in a similar notation would read

with the only difference that of course there is no specific time dependence in Newton’s equations of gravity, so we only have

To make a connection with Abramowitz and Stegun, their x becomes
our time t, their y becomes our position vector 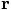 , and their f becomes
our acceleration vector
, and their f becomes
our acceleration vector 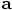 .
Also, their
.
Also, their 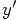 becomes our
velocity vector
becomes our
velocity vector 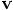 . Finally,
their h is our time step dt.
. Finally,
their h is our time step dt.
Alice: Let us rewrite their set of equations in terms of the
dictionary you just provided. And instead of dt it is better to
write 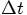 , since dt
is not an infinitesimal quantity here, but a finite time interval. This
then gives us:
, since dt
is not an infinitesimal quantity here, but a finite time interval. This
then gives us:
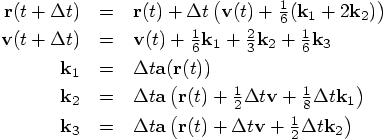
In order to make a connection with your code, we can define three variables
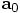 ,
, 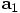 , and
, and 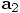 as follows, taking the right hand sides of
the last three equations above, but without the
as follows, taking the right hand sides of
the last three equations above, but without the 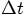 factor:
factor:
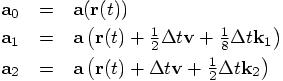
Comparing this with the definitions of 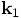 ,
, 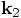 , and
, and 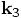 , we can eliminate all
, we can eliminate all 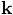 values from the right hand side:
values from the right hand side:
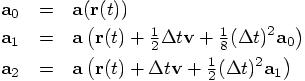
And indeed, these are exactly the three variables a0, a1, and a2, that are computed in your rk4 method.
We can now rewrite the first two of Abramowitz and Stegun’s equations as:
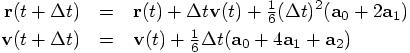
And these correspond precisely to the last two lines in your rk4 method.
Bob: Yes, that was how I derived my code, but I must admit, I did not write it down as neatly and convincingly as you just did.
Alice: So yes, you have indeed implemented Abramowitz and
Stegun’s fourth-order Runge Kutta scheme. But wait a minute, what you
found here, equation 22.5.22, shows a right-hand side with a stated energy
error of order 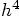 —
which would suggest that the scheme is is only third-order accurate.
—
which would suggest that the scheme is is only third-order accurate.
Bob: Hey, that is right. If you make 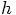 smaller, the number of steps will go up
according to
smaller, the number of steps will go up
according to 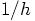 , and
therefore the total error for a give problem will grow proportionally to
, and
therefore the total error for a give problem will grow proportionally to
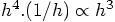 . This would indeed imply
that this method is third-order. But that would be very unusual. In all
text books I’ve seen, you mostly come across second-order and
fourth-order Runge Kuttas. While you certainly can construct a third-order
version, I wouldn’t have expected Abramowitz and Stegun to feature
one. Besides, look at the last expression for the velocity. Doesn‘t
that resemble Simpson’s rule, suggesting fourth-order accuracy.
I’m really puzzled now.
. This would indeed imply
that this method is third-order. But that would be very unusual. In all
text books I’ve seen, you mostly come across second-order and
fourth-order Runge Kuttas. While you certainly can construct a third-order
version, I wouldn’t have expected Abramowitz and Stegun to feature
one. Besides, look at the last expression for the velocity. Doesn‘t
that resemble Simpson’s rule, suggesting fourth-order accuracy.
I’m really puzzled now.
Alice: Could it be a misprint?
Bob: Anything is possible, though here that is not very likely. This is such a famous book, that you would expect the many readers to have debugged the book thoroughly.
Alice: Let’s decide for ourselves what is true and what is not.
Bob: Yes. And either way, whatever the outcome, it will be a good exercise for the students. Let’s first test it numerically.
Alice: Fine with me. But then I want to derive it analytically as well, to see whether we really can understand the behavior of the numerical results from first principles.
Comparing the Four Integrators
Bob: Let us start again with a time step of 0.001, for a duration of ten time units.
Alice: Just to compare, why don’t you run them for all four schemes.
Bob: I am happy to do so. And while we are not sure yet whether our higher-order Runge-Kutta scheme is 3rd order or 4th order, let me continue to call it 4th order, since I’ve called it rk4 in my code. If it turns out that it is 3rd order, I’ll go back and rename it to be rk3.
Alice: Fair enough.
Bob: Okay: forward Euler, leapfrog, 2nd order R-K, and hopefully-4th order R-K:
|gravity> ruby integrator_driver2d.rb < euler.in
dt = 0.001
dt_dia = 10
dt_out = 10
dt_end = 10
method = forward
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 10000 steps :
E_kin = 0.0451 , E_pot = -0.495 , E_tot = -0.45
E_tot - E_init = 0.425
(E_tot - E_init) / E_init =-0.486
1.0000000000000000e+00
2.0143551288236803e+00 1.6256533638564666e-01
-1.5287552868811088e-01 2.5869644289548283e-01
Alice: Ah, this is the result from the forward Euler algorithm, because the fifth line of the output announces that this was the integration method used. As we have seen before, energy conservation has larger errors. We have an absolute total energy error of 0.425, and a relative change in total energy of -0.486. I see that you indeed used dt = 0.001 from what is echoed on the first line in the output. And yes, for these choices of initial conditions and time step size we had seen that things went pretty badly.
Bob: The leapfrog does better:
|gravity> ruby integrator_driver2e.rb < euler.in
dt = 0.001
dt_dia = 10
dt_out = 10
dt_end = 10
method = leapfrog
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 10000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = 3.2e-07
(E_tot - E_init) / E_init =-3.65e-07
1.0000000000000000e+00
5.9946121055215340e-01 -3.6090779482156415e-01
1.0308896785838775e+00 2.1343145669114691e-01
Alice: Much better indeed, as we had seen before. A relative energy
error of 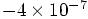 is great, an
error much less than one in a million.
is great, an
error much less than one in a million.
Bob: Time for second-order Runge-Kutta:
|gravity> ruby integrator_driver2f.rb < euler.in
dt = 0.001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk2
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 10000 steps :
E_kin = 0.555 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = 6.02e-05
(E_tot - E_init) / E_init =-6.88e-05
1.0000000000000000e+00
5.9856491479183715e-01 -3.6183772788952318e-01
1.0319067591346045e+00 2.1153690796461602e-01
Alice: Not as good as the leapfrog, but good enough. What I’m curious about is how your hopefully-fourth-order Runge-Kutta will behave.
Bob: Here is the answer:
|gravity> ruby integrator_driver2g.rb < euler.in
dt = 0.001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 10000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = -2.46e-09
(E_tot - E_init) / E_init =2.81e-09
1.0000000000000000e+00
5.9961758437074986e-01 -3.6063455639926667e-01
1.0308068733946525e+00 2.1389536225475009e-01
Alice: What a difference! Not only do we have much better energy
conservation, on the order of a few times 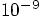 , also the positional accuracy is already on
the level of a few times
, also the positional accuracy is already on
the level of a few times 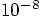 ,
when we compare the output with our most accurate previous runs. And all
that with hardly any waiting time.
,
when we compare the output with our most accurate previous runs. And all
that with hardly any waiting time.
Bob: Yes, I’m really glad I threw that integrator into the menu. The second-order Runge-Kutta doesn’t fare as well as the leapfrog, at least for this problem, even though they are both second-order. But the hopefully-fourth-order Runge-Kutta wins hands down.
Fourth Order Runge-Kutta
Alice: Let’s make the time step ten times smaller:
|gravity> ruby integrator_driver2h.rb < euler.in
dt = 1.0e-04
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 100000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = -8.33e-14
(E_tot - E_init) / E_init =9.52e-14
1.0000000000000000e+00
5.9961755488723312e-01 -3.6063458344261029e-01
1.0308069102701605e+00 2.1389530419780176e-01
Bob: What a charm! Essentially machine accuracy. This makes it pretty obvious that fourth-order integrators win out hands down, in problems like this, over second-order integrators. Higher order integrators may be even faster, but that is something we can explore later.
Alice: Well done. And, by the way, this does suggest that the scheme that you copied from that book is indeed fourth-order. It almost seems better than fourth order.
Bob: Let me try a far larger time step, but a much shorter duration, so that we don’t have to integrate over a complicated orbit. How about these two choices. First:
|gravity> ruby integrator_driver2i.rb < euler.in
dt = 0.1
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.1, after 1 steps :
E_kin = 0.129 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 1.75e-08
(E_tot - E_init) / E_init =-2.01e-08
1.0000000000000000e+00
9.9499478923153439e-01 4.9916431937376750e-02
-1.0020915515250550e-01 4.9748795077019681e-01
And then:
|gravity> ruby integrator_driver2j.rb < euler.in
dt = 0.01
dt_dia = 0.1
dt_out = 0.1
dt_end = 0.1
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 0.1, after 10 steps :
E_kin = 0.129 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 1.79e-12
(E_tot - E_init) / E_init =-2.04e-12
1.0000000000000000e+00
9.9499478009063858e-01 4.9916426216739009e-02
-1.0020902861389222e-01 4.9748796005932194e-01
Alice: The time step went down by a factor 10, and the energy
conservation got better by a factor of almost exactly 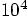 . We really seem to have a fourth order
integration scheme.
. We really seem to have a fourth order
integration scheme.
Bob: This proves it. And I can keep the name rk4, since it lives up to its claim. Good!
Alice: At least it comes close to living up to its name, and it sort-of proves it.
Snap, Crackle, and Pop
Bob: What do you mean with `comes close’? What more proof would you like to have?
Alice: I would still be happier if I could really prove it, with pen and paper, rather than through the plausibility of numerical experimentation.
Bob: Go ahead, if you like!
Alice: Let us take your implementation
def rk4(dt)
old_pos = pos
a0 = acc
@pos = old_pos + vel*0.5*dt + a0*0.125*dt*dt
a1 = acc
@pos = old_pos + vel*dt + a1*0.5*dt*dt
a2 = acc
@pos = old_pos + vel*dt + (a0+a1*2)*(1/6.0)*dt*dt
@vel = vel + (a0+a1*4+a2)*(1/6.0)*dt
end
and let us determine analytically what the first five terms in a Taylor
series in dt look like. We can then see directly whether the error
term is proportional to 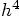 ,
as the book claims, or
,
as the book claims, or 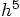 ,
as our calculations indicate.
,
as our calculations indicate.
To start with, let us look at your variable a2, which is the acceleration after a time step dt, starting from an initial acceleration a0. A Taylor expansion can approximate a2 as:
where all the derivatives are understood to be evaluated at the same time
as 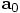 , namely at the
beginning of our time step.
, namely at the
beginning of our time step.
Bob: The first derivative of the acceleration, 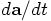 , is sometimes called the jerk. How
about the following notation:
, is sometimes called the jerk. How
about the following notation:

Alice: Fine with me. I believe the term `jerk’ has crept into the literature relatively recently, probably originally as a pun. If a car or train changes acceleration relatively quickly you experience not a smoothly accelerating or decelerating motion, but instead a rather `jerky’ one.
Bob: It may be more difficult to come up with terms for the unevenness in the jerk.
Alice: Actually, I saw somewhere that someone had used the words snap, crackle, and pop, to describe the next three terms.
Bob: As in the rice crispies? Now that will confuse astronomers who did not grow up in the United States! If they haven’t seen the rice crispy commercials, they will have no clue why we would use those names. And come to think of it, I don’t have much of a clue yet either.
Figure 1: Snap, Crackle, and Pop
Alice: Ah, but the point is that the names of these three cheerful characters lend themselves quite well to describe more-than-jerky behavior. After all, the popping of a rice crispy is a rather sudden change of state.
Bob: Okay, now I get the drift of the argument. A sudden snap comes to mind, as a change in jerk. And what changes its state more suddenly than a snap? Well, perhaps something that crackles, although that is pushing it a bit. But a pop is certainly a good word for something that changes high derivatives of positions in a substantial way!
An Attempt at an Analytical Proof
Alice: Okay, let’s make it official:
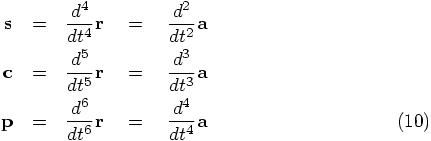
Which turns my earlier equation into:
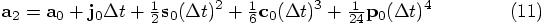
Bob: Much more readable.
Alice: And your other variable a1, which indicates the acceleration after only half a time step, now becomes:
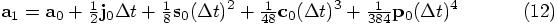
Bob: Ah, and now we can evaluate the last two lines in my rk4 method:
@pos = old_pos + vel*dt + (a0+a1*2)*(1/6.0)*dt*dt
@vel = vel + (a0+a1*4+a2)*(1/6.0)*dt
Alice: Yes. These two lines translate to:
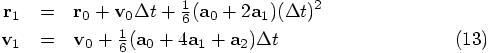
Upon substitution the first line becomes:
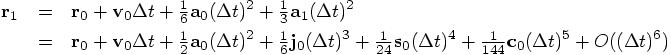
And the second line becomes:
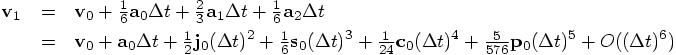
Bob: Very nice. In both cases the terms up to 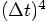 are perfectly correct, and the error starts
in the
are perfectly correct, and the error starts
in the 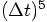 term, where the
Taylor series coefficient would have been
term, where the
Taylor series coefficient would have been 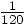 . So the leading error terms are:
. So the leading error terms are:
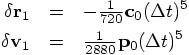
This proves that the rk4 Runge-Kutta method is truly fourth-order, and that there was a typo in Abramowitz and Stegun.
Alice: Or so it seems. But I must admit, I’m not completely comfortable.
Shocked
Bob: Boy, you’re not easy to please! I was ready to declare victory when we had our numerical proof, and you convinced me to do the additional work of doing an analytical check. If it were up to me, I would believe numerics over analytics, any day. Seeing is believing, the proof is in the pudding, and all that.
Alice: Well, it really is better to have both a numerical demonstration and an analytical proof. It is just too easy to be fooled by coincidences or special cases, in numerical demonstrations. And at the same time it is also easy to make a mistake in doing analytical checks. So I think it is only wise to do both, especially with something so fundamental as an N-body integrator.
And I’m glad we did. But something doesn’t quite feel right. Let me just review what we have done. We first expanded the orbit in a Taylor series, writing everything as a function of time. Then we showed that the orbit obeyed the equations of motion, and . . . .
Bob: . . . and then you looked shocked.
Alice: Not only do I look shocked, I am shocked! How could we make such a stupid mistake!?!
Bob: I beg your pardon?
Alice: We assumed that we were sliding along the perfect orbit, and then we proved that we were sliding at the right pace, but we never considered that our numerical orbit is only approximate, and that it will have errors in space as well as in time. So we proved only half of what we should have proved. In other words, we haven’t yet proven anything at all, really!