9. Energy Conservation
Bob: That was quite a long session yesterday, when we were chasing
those bugs while we were trying to implement a better Body class!
Alice: Yes, but we learned a lot about Ruby.
Bob: And even a thing or two about debugging.
Alice: Perhaps this is a good time to return to our real project:
to build progressively better integrators. But before we move on to
second-order integrators, as well as introducing graphics and other
complications, I would like to do one more test. Even though we now
know that our forward Euler scheme converges, we don't know yet how
well it conserves energy. Shouldn't we test that explicitly?
Bob: Great minds think alike. I had come to the same conclusion.
For the two-body problem, of course you can check all kind of things.
You can measure how accurately a bound orbit remains the same ellipse,
as it should be, rather than slowly drifting and changing shape, and
whether the motion traverses the ellipse at the right speed, and so on.
The reason is that we have an analytic solution for the two-body problem.
For the many-body problem in general, however, we are a lot less
lucky. All we know is that the total energy and total angular
momentum of the system are conserved. That gives us one scalar and
one vector, or in three dimensions it gives us four conserved
quantities. In addition, there are the position and velocity of the
center-of-mass motion, which give us another six conserved quantities,
ten in total.
So we cannot compare all the details of the motion of the
However, things are not as bad as they may seem. If you make errors
in your integration, and you always make errors at some level, those
errors will let the simulated orbit drift away from the true orbit in
a random fashion. It would require a very clever conspiracy for those
errors to work together in such a way as to keep the energy conserved
to a high degree of accuracy, while still introducing much larger errors
elsewhere. In practice, therefore, checking energy conservation in an
N-body system has become the standard test to see how
accurate the integration of an N-body system is.
Alice: Another way of saying this is to picture the phase space of
the whole system.
Bob: You mean the six-dimensional space in which you plot for each
particle its position and velocity?
Alice: I was thinking about the alternative way of picturing the whole
system as one point in a
Bob: Which reaches the same conclusion as what I just summarized.
Alice: Yes. Since the dynamics of this one point in
Bob: More mathematically minded students might prefer your explanation;
I think I'll just stick to my more lowbrow explanation. But however
we tell the story, we should of course warn them that this argument
fails when we are dealing with an integrator that has a built-in type
of energy conservation.
Alice: Yes, indeed, that is very important. It would be easy to
construct an integrator that projects the orbit of the master particle
in
Bob: Or the way I would put it, you could just wiggle one particle
far out, perhaps a particle that has already escaped from the system.
By changing the velocity of that particle a little, you will change
its kinetic energy, and so you can accurately balance the numerical
errors that occur in the rest of the system. But of course that does
not make the rest of the system behave in a more accurate way.
Alice: Of course, the two examples that you and I just cooked up
are extreme. It is not at all a bad idea to conserve energy, if your
approach is part of a systematic way to make the whole integration
more accurate. Symplectic integrators are an example.
Bob: I have heard of the name, but I must admit I don't know what they
are.
Alice: They are a lot of fun, from a mathematical point of view.
How useful they may be for real N-body simulations, that is not too
clear. They are more accurate, for sure, but they are hard to
generalize to individual time steps. And for our game, we have no
other choice but to go to individual time steps. Perhaps we can come
back to this topic, some day, but not any time soon. But just to give
you one example of the simplest symplectic integrator: the good old
leapfrog scheme, also known in some areas of physics as the Verlet
algorithm.
Bob: Which is probably the next algorithm we want to implement.
Alice: Yes. So shall we first test energy conservation of our
forward Euler code?
Bob: Well, I have a surprise for you. Last night I continued
to tinker with Ruby, and I had so much fun doing so that I stayed
at it long enough to wind up with a version of our code that produces
energy conservation diagnostics.
Alice: How nice! Can I see it?
Bob: First of all, here is the driver, in file euler.rb,
the only part of the program that we will change, while exploring the
effect of different time step sizes and integration times:
Alice: So at the bottom you create a new particle, which will represent
the relative motion between the two bodies in our system, with the call to
Body.new, then you read in the initial conditions, as we did
before, and then you tell the particle to evolve itself.
Bob: Yes, with evolve I mean that we invoke here a method that computes
the evolution of the system in time. I have made this a method
in the Body class, so we can invoke it with b.evolve.
The only extra thing needed is to tell the particle how long to integrate,
with what time step, and how frequently to report the degree of energy
conservation and the actual position and velocity of the relative motion.
Alice: So the actual program is a mere three lines, at the bottom, with
the four lines of assignments at the top just the way to specify each of
those four parameters you just mentioned.
Bob: Exactly. Ruby is very economical! And just as a courtesy, I
decided to let the program print out the values of the four parameters.
We can then change those parameters in the current file to our hearts'
content, and we can always check from earlier outputs what parameters were
used for a given integration.
Alice: Good idea. Clean and careful. Of course, some day soon we will
want to give those values as command line options, rather than always editing
the file.
Bob: I suppose so, although we'll have to think about that. It is of
course possible to give Unix-style command line options, but there are
several other ways as well; in fact Ruby has a nice built-in way to do
that.
Alice: Later. Can I have a look at what the Body class now looks like?
It must have grown quite a bit, since it now contains not only the forward
Euler integrator, but also your whole evolve method, as well as whatever
you wrote to get all the energy diagnostics done.
Bob: It's not that bad, actually. Ruby really is a compact language.
Here, let me show you the whole file body.rb first, and then
we can go through each of the methods used.
9.1. Estimating Numerical Errors
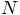 particles with theory, not by a long shot. An
N-body system in three dimensions has
particles with theory, not by a long shot. An
N-body system in three dimensions has 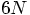 degrees of freedom, far more than the 10 handles we have in our 2-body case.
degrees of freedom, far more than the 10 handles we have in our 2-body case.
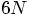 -dimensional system. The
evolution of an N-body system can then be viewed as the
complex motion of this one point through this huge space. Now in this
space you can define layers of subspaces, on each of which the total
energy of the system is constant. Once the particle starts on such a
hypersurface, it should stay there, because energy is conserved. But
if we make arbitrary errors in computing its motion, our simulated
particle will show some numerical drift in all dimensions available,
including the direction perpendicular to the energy hypersurface.
-dimensional system. The
evolution of an N-body system can then be viewed as the
complex motion of this one point through this huge space. Now in this
space you can define layers of subspaces, on each of which the total
energy of the system is constant. Once the particle starts on such a
hypersurface, it should stay there, because energy is conserved. But
if we make arbitrary errors in computing its motion, our simulated
particle will show some numerical drift in all dimensions available,
including the direction perpendicular to the energy hypersurface.
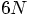 dimensions is incredibly complicated, the distance away from the energy
hypersurface will typically be of the same order of magnitude as the
total length of the drift of that master particle that symbolizes our
whole N-body system.
dimensions is incredibly complicated, the distance away from the energy
hypersurface will typically be of the same order of magnitude as the
total length of the drift of that master particle that symbolizes our
whole N-body system.
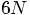 dimensions back onto the original constant-energy
hypersurface. But that would be cheating. It would get rid of only
one degree of freedom of the total error, and leave the other
dimensions back onto the original constant-energy
hypersurface. But that would be cheating. It would get rid of only
one degree of freedom of the total error, and leave the other
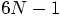 degrees of freedom uncorrected. It would look great
when you test for energy conservation, but at the cost of having lost
your handle on checking what is going on.
degrees of freedom uncorrected. It would look great
when you test for energy conservation, but at the cost of having lost
your handle on checking what is going on.
9.2. A Driver