5. The Two-Body Problem
Alice: That was great, to be able to do such rapid prototyping in a
language we hardly knew. I can see the advantages of an interpreted,
dynamically typed computer language. If we had tried to do this in C++,
it would have taken quite a bit more time, and we would have had to write
many more lines of code.
Bob: Yes. Defining a class, getting it to behave, providing I/O, and
chaining it together by piping data from one program to another, all
that is a nontrivial beginning. This is encouraging! Let's move on,
to see how much we have to add before we can let the integrator
integrate.
Alice: Not much, I think, at least if we start with the simplest
integrator possible, forward Euler, for the simplest N-body system,
namely to solve the 2-body problem.
Bob: The other day I was asked by a friend outside astronomy why we
call it the N-body problem. What was the problem with those bodies,
she asked. I had to think for a moment, because we are just in the
habit to talk about it that way.
Alice: We talk about solving the equations of motion; normally when
you solve something, you solve a problem. I guess the terminology
comes from seeing a differential equation as posing a problem, that
you then solve, either analytically or numerically. Newton's equations
of motion for N bodies form a system of N differential equations, and
the challenge to obtain solutions is called the N-body problem.
I must admit, I don't like the term "N-body" at all. Why N, and not
some other symbol? I would much rather use the term "many body", as
they do in solid state physics, say. Don't you agree that the
"gravitational many-body problem" sounds much more elegant than the
"gravitational N-body problem"?
Bob: I really don't care, as long as I can solve it. Okay, let's
start with the 2-body problem, which is really a 1-body problem of
course, since you only have to solve the relative motion between the
two particles.
Alice: You say "of course", but if this is going to be a presentation
for students, we'd better be more explicit. We should start with
Newton's equations of motion for a gravitational many-body system:
Here
For a 2-body system, everything simplifies a lot. Instead of dealing
with position
This can be visualized as a vector pointing from particle 1 to particle
2, in other words with its head at the position of particle 2, and its
tail at the position of particle 1.
Introducing
We can choose physical units for mass, length, and time in such a way
that
You often see an even more abbreviated `dot' notion for time derivatives.
If we place a dot on top of a variable for each time derivative we take,
we wind up with
Bob: End of lecture. Yes, let's start solving that last equation.
Here is how the forward Euler integration scheme works:
for the position
Of course, we have to provide intial conditions for the position and
velocity vectors, before we can solve the equations, and we will do
that as soon as we have a working integrator. For now, all we have
to do is to code up these equations.
Alice: That was an even shorter lecture. Yes, let's do it.
Bob: Shall we type the code in the same file test.rb where
we put the Body class? We can still use the Body format for our
`relative' particle, as long as we remember that the mass of that
particle corresponds to the sum of the masses of the original particle.
Alice: We can certainly use the Body class, but I suggest that we
put the definition of the Body class in a file body.rb, and
only the actual integrator in our file test.rb.
Bob: A modular approach, I take it?
Alice: Sure, whenever I can get away with it!
Bob: It may not be a bad idea, in this case. And to show you how
modular I can be, I will even call my first attempt body0.rb.
When we create other versions, we can give them higher numbers, and when
we are really happy, we can call the final version body.rb.
Alice: That sort-of goes in a modular direction. It all depends
on what you do with that stack of versions. But I appreciate your
attempt!
Bob: Coming back to your suggestion, yes, we can put the Body
class definition in a separate file. This is similar to what you do
in C and C++ with an include file -- only here it is easier to do so.
Alice I remember well those constructs in C where you had to write things
like #ifndef this and #ifndef that before you could
be sure that it was safe to include a file without including it more than
once? You're saying that Ruby makes life easier?
Bob: Yes, in Ruby you can use a construct called require
"filename": it only includes the file if it hasn't been
included yet, directly or indirectly.
Here is the file body0.rb:
It is just as we left it, but without my one-liner I/O hacks. Now
give me some time to figure out how to implement the forward Euler
idea . . . .
. . . Here it is, the new version of test.rb. As you can
see, it starts with requiring that body0.rb gets included at
the top.
Alice: Short and simple, but it looks simple only because we are used
to coding up integrators. For the students, it would be good to spell
out, just one time, what the equations above look like, in the simplest
case where we are working with vectors in two dimensions. To be specific
in our notation, we can use subscript x for the first component of
each vector and subscript y for the second component, as follows:
The last three equations in the earlier sections then become six
equations, one for each vector component.
There are two equations for the calculation of the relative
acceleration components
Two equations tell us how to find the position vector components at
the new time step: we take the components at the previous time, and
we add the increment in position provided by the product of the
corresponding velocity vector component and the time step size:
Similarly, we update the velocity vector components, by incrementing
those using the acceleration, which is the time derivative of the velocity:
If we would do this calculation in three-dimensional space, all vectors
would acquire a third component:
To conclude the story, the forward Euler algorithm for the two-body
problem can be summarized as follows. Given the relative position and
the relative velocity between the two particles at a given time
Bob: And after you have once said that in words, it becomes obvious
how much more compact and efficient equations are in
component notation. And then it is clear that vector notation is even
more efficient than component notation.
5.1. Equations of Motion
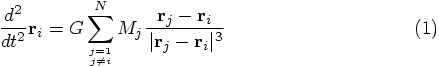
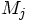 and
and 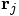 are the mass and
position vector of particle
are the mass and
position vector of particle 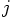 , and
, and 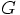 is the
gravitational constant. To bring out the inverse square nature of
gravity, we can define
is the
gravitational constant. To bring out the inverse square nature of
gravity, we can define
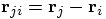 , with
, with
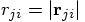 , and unit vector
, and unit vector
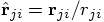 . The
gravitational acceleration on particle
. The
gravitational acceleration on particle 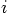 then becomes:
then becomes:

5.2. Relative Motion
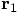 for the first particle and
for the first particle and
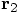 for the second particle, we can write the
above system of equations of motion as a single equation instead, in
terms of the relative position, defined as:
for the second particle, we can write the
above system of equations of motion as a single equation instead, in
terms of the relative position, defined as:

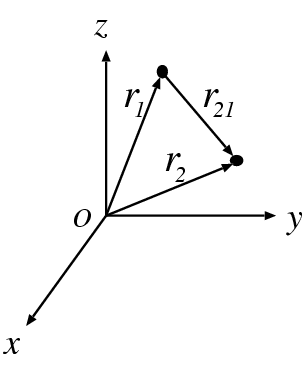
 , we then get:
, we then get:
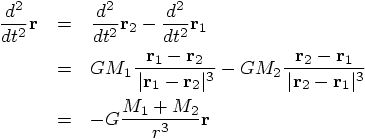
 . With the shorter notation
. With the shorter notation  ,
we then get
,
we then get


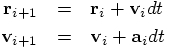
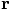 , the velocity
, the velocity 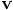 , and
the acceleration
, and
the acceleration 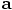 of our single particle, that describe
aspects of the relative motion between two particles. The index
of our single particle, that describe
aspects of the relative motion between two particles. The index
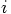 indicates the values for time
indicates the values for time 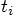 and
and
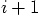 for the time
for the time 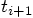 after one more time
step has been taken:
after one more time
step has been taken: 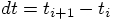 .
.
5.3. Modularity
5.4. The First Integrator

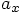 and
and 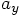 ,
each of which can be calculated in terms of the relative position
components
,
each of which can be calculated in terms of the relative position
components 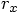 and
and 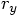 , since
, since
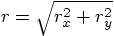 :
:
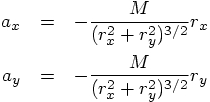
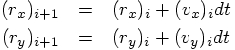
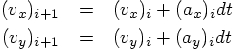
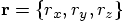 ,
and so on. Each pair of equations above would then be replaced by a
triple of equations, because an extra equation would appear for the
corresponding
,
and so on. Each pair of equations above would then be replaced by a
triple of equations, because an extra equation would appear for the
corresponding 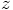 component.
component.
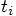 , first calculate the relative acceleration in terms
of the relative position at
, first calculate the relative acceleration in terms
of the relative position at 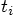 . Then compute the new
values for the relative positions at
. Then compute the new
values for the relative positions at 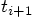 , in terms of
the relative positions and velocities at
, in terms of
the relative positions and velocities at 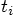 .
Similarly, compute the new values for the relative velocities at
.
Similarly, compute the new values for the relative velocities at
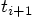 , in terms of the relative velocities and
accelerations at
, in terms of the relative velocities and
accelerations at 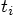 .
.
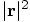 by introducing a variable r2, initialize it to zero, and then
accumulating the result of squaring the value of each component of the
vector
by introducing a variable r2, initialize it to zero, and then
accumulating the result of squaring the value of each component of the
vector 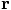 . What you need for the acceleration is
the 3/2 power, so you compute that in the next line.
. What you need for the acceleration is
the 3/2 power, so you compute that in the next line.