1. Performance
Alice: Now that we can build a real star cluster model, with our Plummer's
model generator mkplummer.rb, we're getting closer do some
real physics. I would love to use our N-body code to demonstrate
gravitational thermodynamics effects, such as negative heat capacity.
Bob: Before we can do that, we'll have to speed up our Ruby code
significantly! Right now, we don't stand a chance. We can play with
a few particles, but there is no way we can handle even a few hundred
particles, at this moment.
Alice: Is it that bad?
Bob: It is that bad, yes. Let's do a test, to see how long a single time
step takes, say for 256 particles. I like to run tests with particle
numbers that are powers of 2, to make it easier to compare timings between
different runs.
Alice: Why don't we start more modestly, just to see whether the combination
of our Plummer generator and our N-body code does what it is supposed
to do, say for 8 particles.
Bob: Okay, better safe than sorry. Here we go, for one time unit.
And I'll use a hefty dose of softening, just in case two of the particles
happen to be born very close to each other. Before too long, we should
introduce variable time steps, to handle close encounters. But until we
can teach particles to shrink their time step when they meet each other,
it is better to use an amount of softening that is an order of magnitude
larger than the time step. In that way, not much can change in the
gravitational potential during one time step.
Alice: As long as the velocities are of order one. In practice, particles
will speed up when they come close together.
Bob: Yes, but only with the inverse square root of the distance. So if
we use a softening length of, say, 0.01, we can probably still use a time
step of 0.1 -- but perhaps I'm too optimistic. Let's try it:
Alice: That's not bad, as far as energy conservation is concerned. I see
that you used a random seed for the random number generator. Let's
try another run, to see how large the variations in energy conservation
are, for different Plummer's model realizations.
Bob: I prefer to suppress the snapshot output, now that we have seen that
reasonable numbers are produced. I'll just ask for a snapshot output time
that is longer than the run time:
Bob: Fine, but all that output is too much of a good thing, for my taste.
Let me suppress the initial state echo. Since all that stuff appears on the
standard error stream, I'll have to add a & symbol to a
pipe, in order to get both streams through, the standard output and
the standard error stream. I'll then just ask for the very last line with
tail -1 :
Alice: Quite a bit of run-to-run variation of the energy errors.
Can you try a few more?
Bob: Now it's easy:
Bob: Let's create a standard input file, so that we can do some timings.
Alice: Timing should be independent of energy error, since the number of
integration steps are the same for different Plummer realizations.
Bob: That's true, but I like to make the command line a bit shorter.
Here is one standard input file, for 8 particles:
Alice: Perhaps a matter of wrapping it up within parentheses again?
Bob: That may wel work:
1.1. A Matter of Speed
|gravity> ruby mkplummer.rb -n 8 | ruby nb1.rb -t 1 -d 0.01 -s 0.1
ruby: No such file or directory -- mkplummer.rb (LoadError)
/home/makino/papers/acs/lib/clop.rb:310: warning: already initialized constant HELP_DEFINITION_STRING
==> The simplest ACS N-body code <==
Integration method : rk4
Integration time step : dt = 0.01
Diagnostics output interval : dt_dia = 1.0
Snapshot output interval : dt_out = 1.0
Duration of the integration : dt_end = 1.0
Softening length : eps = 0.1
./nbody1.rb:167:in `/': divided by 0 (ZeroDivisionError)
from ./nbody1.rb:167:in `write_diagnostics'
from ./nbody1.rb:86:in `evolve'
from nb1.rb:144
1.2. Energy Conservation
|gravity> ruby mkplummer.rb -n 8 | ruby nb1.rb -t 1 -d 0.01 -s 0.1 -o2
ruby: No such file or directory -- mkplummer.rb (LoadError)
/home/makino/papers/acs/lib/clop.rb:310: warning: already initialized constant HELP_DEFINITION_STRING
==> The simplest ACS N-body code <==
Integration method : rk4
Integration time step : dt = 0.01
Diagnostics output interval : dt_dia = 1.0
Snapshot output interval : dt_out = 2.0
Duration of the integration : dt_end = 1.0
Softening length : eps = 0.1
./nbody1.rb:167:in `/': divided by 0 (ZeroDivisionError)
from ./nbody1.rb:167:in `write_diagnostics'
from ./nbody1.rb:86:in `evolve'
from nb1.rb:144
Alice: Indeed, a different energy error. Let's try a few more.
|gravity> ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2 |& tail -1
ruby: No such file or directory -- mkplummer.rb (LoadError)
from nb1.rb:144
Oops, I forget that the mkplummer command generates its own initial
state messages. But I can take care of that by wrapping both commands in
a set of parentheses:
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
Much better!
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
|gravity> (ruby mkplummer.rb -n8 | ruby nb1.rb -t1 -d0.01 -s0.1 -o2) |& tail -1
from nb1.rb:144
Alice: Your abbreviation techniques do make it easier to see
what is going on. In any case, a time step of 0.01 does not seem to large
for a softening of 0.1
1.3. Timing
|gravity> ruby mkplummer.rb -n 8 -s 42 > plum8.in
ruby: No such file or directory -- mkplummer.rb (LoadError)
Let me try to obtain some timing information:
|gravity> time ruby nb1.rb -t1 -d0.01 -s0.1 -o2 < plum8.in
/home/makino/papers/acs/lib/clop.rb:310: warning: already initialized constant HELP_DEFINITION_STRING
==> The simplest ACS N-body code <==
Integration method : rk4
Integration time step : dt = 0.01
Diagnostics output interval : dt_dia = 1.0
Snapshot output interval : dt_out = 2.0
Duration of the integration : dt_end = 1.0
Softening length : eps = 0.1
./nbody1.rb:167:in `/': divided by 0 (ZeroDivisionError)
from ./nbody1.rb:167:in `write_diagnostics'
from ./nbody1.rb:86:in `evolve'
from nb1.rb:144
0.032u 0.007s 0:00.03 100.0% 0+0k 0+0io 0pf+0w
Again, I prefer to suppress most of the information here:
|gravity> time ruby nb1.rb -t1 -d0.01 -s0.1 -o2 < plum8.in |& tail -2
from ./nbody1.rb:86:in `evolve'
from nb1.rb:144
Ah, that threw away too much: the timing information went down the drain.
|gravity> (time ruby nb1.rb -t1 -d0.01 -s0.1 -o2 < plum8.in) |& tail -2
from nb1.rb:144
0.023u 0.003s 0:00.02 100.0% 0+0k 0+0io 0pf+0w
Alice: And so it does.
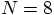 , let us try the
, let us try the 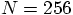 that I
suggested earlier.
that I
suggested earlier.
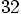 , which means that the number of
particle-particle interactions increase by a factor
, which means that the number of
particle-particle interactions increase by a factor 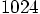 ,
the square of
,
the square of 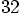 .
.
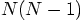 , which gives us a factor
of
, which gives us a factor
of 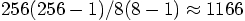 . And besides, there
is the overhead of reading in the particles, printing them out, and various
other overhead that is linear, rather than quadratic in
. And besides, there
is the overhead of reading in the particles, printing them out, and various
other overhead that is linear, rather than quadratic in 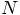 .
.
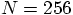 run to take
a factor of a thousand more time. So far, we have followed the
run to take
a factor of a thousand more time. So far, we have followed the
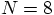 run for 100 time steps. So a single time step for a
run for 100 time steps. So a single time step for a
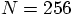 run should take about ten times longer than our
run should take about ten times longer than our
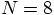 runs.
runs.
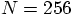 , it would take a day to run a decent experiment.
No, we can't wait that long.
, it would take a day to run a decent experiment.
No, we can't wait that long.
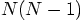 fashion.
We can already gain almost a factor of two by computing the acceleration
of particle i by particle j at the same time that we compute the
acceleration of particle j by particle i since the intermediate steps
are the same. This will reduce the number of square root calls from
fashion.
We can already gain almost a factor of two by computing the acceleration
of particle i by particle j at the same time that we compute the
acceleration of particle j by particle i since the intermediate steps
are the same. This will reduce the number of square root calls from
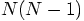 to
to 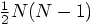 per time step. Since
square roots are more expensive than additions and multiplications,
this is bound to help.
per time step. Since
square roots are more expensive than additions and multiplications,
this is bound to help.