3. A Puzzle
Bob: We can now put our distance measurement tool to good use, by
testing whether our shared time step integrator really does the right
thing.
We'll do a test run with the constant time step code first,
and then compare the results with that from the shared time step
code.
Alice: Let's take an unusual integrator. How about the good old
fourth order Runge-Kutta scheme?
Bob: As you wish. And while we're at it, let's check whether the scheme
is still fourth order, in constant as well as shared time step form. First
I'll prepare initial conditions with the particles all properly numbered:
Alice: Let's ask our clop function to provide them:
Bob: Aha, now I remember. Okay, how about this?
Alice: Well, that doesn't look like a fourth-order behavior. The second
run was far too accurate, as if it were a fifth-order algorithm. The reason
may well be that running constant time steps in a system where particles
are allowed to come arbitrarily close to each other is not a good
thing. We really should have used softening.
Bob: That's easy to test. Here you are:
Alice: Hmm, that's surprising. In any case, we don't want to use softening
in our shared time step code, so we should find a reasonable run for
our constant time step code without softening. How about making the total
time integration ten times shorter?
Bob: I'm all for speeding things up. Here is the original set, now
shortened:
Before we go any further, and use our shared time step integrator, let's
first see whether in this case the distance in phase space also scales
like the fourth power in the time step.
Bob: Ah, yes, good idea. But in order to do so, we have to know what the
`true' solution is. When we check energy conservation, we know that a
truly accurate integration would give us an energy error of zero, but when
we compare the two outputs we just got, we need to compare them to an even
more accurate soluation. Well, we can run our code with a much smaller
time step, and declare that the result should be close to `true'. Or to
speed things up a bit, we can take a higher-order integrator. Why not
throw the sixth-oder Yoshida version in, to help us:
Bob: After all these preliminaries, we can finally test our shared time
step code:
Alice: I guess that is the price we have to pay for constructing a
more robust code.
Bob: Yes, that must be the case. In general, when you're developing a
more complex algorithm, you have to pay an initial price of a reduce
efficiency.
But we had no choice. In fact, we were lucky that we got such a good
result with a constant time step code, without using any softening.
If we would have repeated those runs with other Plummer realizations,
sooner or later we would have found ourselves in a situation in which
two particles have a close encounter at a distance less than the step
size, leading to huge errors. That at least cannot happen in our
shared time step code, where the adaptive time step determination
would always shrink the time step to be much less than the encounter
time.
Alice: This may be the first time I've heard you arguing eloquently
for reducing efficiency!
Bob: Only when necessary! Now let's see whether we're getting equally
close to the `true' run in phase space:
Bob: That sure doesn't look good. How can the distance be so large?
Alice: Let's go back to basics, and do the same thing with the leapfrog
integrator instead. And since we'll have lower accuracy, we may as well
go to a comparison with time steps that are a factor of ten smaller; we
won't have to be afraid to run into round-off errors:
Alice: And, really, the phase space distance should also become a
hundred times better. Let's see whether it does:
Bob: No, it doesn't. Given the fact that energy conservation was
scaling so perfectly like second-order, it is very hard to believe
that the individual positions and velocities wouldn't scale in the
same way. What is going on here?
Alice: Let's completely forget about higher-order integrators, and
stick to the basics completely. If we do a third leapfrog integration,
we can use the result of that run as our yard stick:
Alice: And even if it were quadratic, I'm still worried about the large
magnitude of the phase space distance for our fourth-order integrator.
And in fact, these leapfrog phase space distances are also larger than
I would have expected.
Bob: All this should tell us something. But what?
Alice: Beats me.
Bob: This is ennoying. Just when we were having fun!
Alice: How about a cup of tea first?
Bob: Feel free to get some tea, but I'll stay here. I just can't stand
this. What could be going so terribly wrong here? 3.1. Starting with Runge-Kutta
|gravity> kali mkplummer.rb -n 4 -s 1 | kali nbody_set_id.rb > test.in
==> Plummer's Model Builder <==
Number of particles : N = 4
pseudorandom number seed given : 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
actual seed used : 1
==> Takes an N-body system, and gives each body a unique ID <==
value of @body_id for 1st body : n = 1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
Starting with the constant time step version, let's choose the
rk4 integrator, but what options did we use for algorithm
choice? I always forget what names we gave our options.
|gravity> kali nbody_cst1.rb -h
Constant Time Step Code
-g --integration_method: Integration method [default: hermite]
-s --softening_length : Softening length [default: 0.0]
-c --step_size : Time step size [default: 0.001]
-d --diagnostics_interval: Interval between diagnostics output [default: 1]
-o --output_interval : Time interval between snapshot output [default: 1]
-t --duration : Duration of the integration [default: 10]
-i --init_out : Output the initial snapshot
--verbosity : Screen Output Verbosity Level [default: 1]
--acs_verbosity : ACS Output Verbosity Level [default: 1]
--precision : Floating point precision [default: 16]
--indentation : Incremental indentation [default: 2]
-h --help : Help facility
---help : Program description (the header part of --help)
3.2. Energy Scaling
|gravity> kali nbody_cst1.rb -g rk4 -t 1 < test.in > rk4cst.out
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.0
Time step size : dt = 0.001
Interval between diagnostics output: dt_dia = 1.0
Time interval between snapshot output: dt_out = 1.0
Duration of the integration : t = 1.0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 1000 steps :
E_kin = 0.289 , E_pot = -0.576 , E_tot = -0.287
E_tot - E_init = -0.0368
(E_tot - E_init) / E_init = 0.147
Now let's make the time step two times smaller
|gravity> kali nbody_cst1.rb -g rk4 -t 1 -c 0.0005 < test.in > rk4cst_half.out
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.0
Time step size : dt = 0.0005
Interval between diagnostics output: dt_dia = 1.0
Time interval between snapshot output: dt_out = 1.0
Duration of the integration : t = 1.0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 2000 steps :
E_kin = 0.312 , E_pot = -0.563 , E_tot = -0.252
E_tot - E_init = -0.00155
(E_tot - E_init) / E_init = 0.00621
3.3. Phase Space Distance Scaling
|gravity> kali nbody_cst1.rb -s 0.01 -g rk4 -t 1 -c 0.001 < test.in > /dev/null
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.01
Time step size : dt = 0.001
Interval between diagnostics output: dt_dia = 1.0
Time interval between snapshot output: dt_out = 1.0
Duration of the integration : t = 1.0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 1000 steps :
E_kin = 0.339 , E_pot = -0.589 , E_tot = -0.25
E_tot - E_init = -0.00011
(E_tot - E_init) / E_init = 0.00044
|gravity> kali nbody_cst1.rb -s 0.01 -g rk4 -t 1 -c 0.0005 < test.in > /dev/null
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.01
Time step size : dt = 0.0005
Interval between diagnostics output: dt_dia = 1.0
Time interval between snapshot output: dt_out = 1.0
Duration of the integration : t = 1.0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 2000 steps :
E_kin = 0.339 , E_pot = -0.589 , E_tot = -0.25
E_tot - E_init = -3.58e-06
(E_tot - E_init) / E_init = 1.43e-05
It still behaves like a fifth-order scheme, with an improvement of
about a factor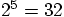 
instead of the expected 
.
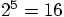|gravity> kali nbody_cst1.rb -g rk4 -t 0.1 -d 0.1 -o 0.1 < test.in > rk4cst.out
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.0
Time step size : dt = 0.001
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.1, after 100 steps :
E_kin = 0.337 , E_pot = -0.587 , E_tot = -0.25
E_tot - E_init = 1.22e-11
(E_tot - E_init) / E_init = -4.9e-11
|gravity> kali nbody_cst1.rb -g rk4 -c 0.0005 -t 0.1 -d 0.1 -o 0.1 < test.in > rk4cst_half.out
==> Constant Time Step Code <==
Integration method : method = rk4
Softening length : eps = 0.0
Time step size : dt = 0.0005
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.1, after 200 steps :
E_kin = 0.337 , E_pot = -0.587 , E_tot = -0.25
E_tot - E_init = 7.65e-13
(E_tot - E_init) / E_init = -3.06e-12
Alice: And now it scales indeed like fourth order. I don't like the fact
that we don't have a good explanation for this phenomenon, but I guess the
only thing that is really guaranteed in an integration scheme is that things
scale at least as good as the order they are supposed to have. For now, let
us test things with the shorter run.
|gravity> kali nbody_cst1.rb -g yo6 -t 0.1 -d 0.1 -o 0.1 < test.in > yo6cst.out
==> Constant Time Step Code <==
Integration method : method = yo6
Softening length : eps = 0.0
Time step size : dt = 0.001
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.1, after 100 steps :
E_kin = 0.337 , E_pot = -0.587 , E_tot = -0.25
E_tot - E_init = 6.66e-16
(E_tot - E_init) / E_init = -2.66e-15
First we'll compare the first run with the `true' run:
|gravity> cat rk4cst.out yo6cst.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 4.1901622499486129e-11
And then we'll take the second run, to compare it with the `true' one:
|gravity> cat rk4cst_half.out yo6cst.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 2.6148912779835136e-12
Alice: Very nice indeed, almost exactly a factor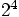 
smaller.
3.4. The Shared Time Step Code
|gravity> kali nbody_sh1.rb -g rk4 -t 0.1 -d 0.1 -o 0.1 < test.in > rk4sh.out
==> Shared Time Step Code <==
Integration method : method = rk4
Parameter to determine time step size: dt_param = 0.01
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.101356, after 54 steps :
E_kin = 0.339 , E_pot = -0.589 , E_tot = -0.25
E_tot - E_init = 1.08e-10
(E_tot - E_init) / E_init = -4.33e-10
Not quite as accurate as the comparable run for constant step size, even
though we used slightly more steps.
|gravity> cat rk4sh.out yo6cst.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 1.0329426107637865e-02
Alice: What is that?!?
3.5. Back to Basics
|gravity> kali nbody_sh1.rb -g leapfrog -t 0.1 -d 0.1 -o 0.1 < test.in > leap_sh.out
==> Shared Time Step Code <==
Integration method : method = leapfrog
Parameter to determine time step size: dt_param = 0.01
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.101356, after 54 steps :
E_kin = 0.339 , E_pot = -0.589 , E_tot = -0.25
E_tot - E_init = 4.37e-06
(E_tot - E_init) / E_init = -1.75e-05
|gravity> kali nbody_sh1.rb -g leapfrog -c 0.001 -t 0.1 -d 0.1 -o 0.1 < test.in > leap_sh_ten.out
==> Shared Time Step Code <==
Integration method : method = leapfrog
Parameter to determine time step size: dt_param = 0.001
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.100043, after 533 steps :
E_kin = 0.337 , E_pot = -0.587 , E_tot = -0.25
E_tot - E_init = 4.21e-08
(E_tot - E_init) / E_init = -1.68e-07
Bob: The energy scales like it should for a second-order integrator:
a hundred times better accuracy for a ten times smaller time step.
|gravity> cat leap_sh.out yo6cst.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 1.0345228714373102e-02
|gravity> cat leap_sh_ten.out yo6cst.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 3.2682294682812577e-04
3.6. Even more Basic
|gravity> kali nbody_sh1.rb -g leapfrog -c 0.0001 -t 0.1 -d 0.1 -o 0.1 < test.in > leap_sh_hundred.out
==> Shared Time Step Code <==
Integration method : method = leapfrog
Parameter to determine time step size: dt_param = 0.0001
Interval between diagnostics output: dt_dia = 0.1
Time interval between snapshot output: dt_out = 0.1
Duration of the integration : t = 0.1
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.5 , E_tot = -0.25
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.100012, after 5330 steps :
E_kin = 0.337 , E_pot = -0.587 , E_tot = -0.25
E_tot - E_init = 4.2e-10
(E_tot - E_init) / E_init = -1.68e-09
|gravity> cat leap_sh.out leap_sh_hundred.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 1.0255420353990194e-02
|gravity> cat leap_sh_ten.out leap_sh_hundred.out | kali nbody_diff.rb
==> 6N-dimensional phase space distance between two N-body systems <==
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
6N-dim. phase space dist. for two 4-body systems: 2.3701380646332516e-04
Bob: That doesn't make much difference. Still no quadratic behavior.