10. Cold Collapse with Softening
Alice: It's probably a good idea to try our standard check with the
figure-8 three-body system, just to make sure that with zero softening
we get the same results as before.
Bob: Yes, I agree. Here we go:
Alice: Good. Now let's try the same cold collapse as before,
but with a softening length of, say, 0.1. At the beginning of their
free fall, the particles will almost feel the same forces as they did
before. Let us compare it with the run that had a time step of 0.001.
For that case we had a horrible lack of energy conservation. Your
softened code should do a lot better.
Bob: Okay, let us see:
But wait a minute, the energy E_tot at time t = 0 is
the same as before. How can that be? When we change the potential,
there should at least be some change in the value of the initial total
energy.
Bob: Ah, but the particles are all separated by at least 2 length units
from each other. Since the softening always comes in through an expression
containing
Alice: just to make sure, let us take a softening length of 0.3.
According to your analysis, that would show a difference in the
initial total energy, right?
Bob: I would think so. Okay, let's try:
Bob: Yes, it never hurts to check.
Alice: And it hurts a lot if you don't check, and run into mysterious
problems later.
10.1. Check
|gravity> ruby rknbody9a_driver.rb < figure8.in
eps = 0
dt = 0.001
dt_dia = 2.1088
dt_out = 2.1088
dt_end = 2.1088
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 1.21 , E_pot = -2.5 , E_tot = -1.29
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2.109, after 2109 steps :
E_kin = 1.21 , E_pot = -2.5 , E_tot = -1.29
E_tot - E_init = -2e-15
(E_tot - E_init) / E_init = 1.55e-15
3
2.1089999999998787e+00
1.0000000000000000e+00
-1.6047303546488470e-04 -1.9320664965417420e-04
-9.3227640249930266e-01 -8.6473492670753516e-01
1.0000000000000000e+00
9.7020367429337440e-01 -2.4296620300772800e-01
4.6595057278750124e-01 4.3244644507801255e-01
1.0000000000000000e+00
-9.7004320125790211e-01 2.4315940965738195e-01
4.6632582971180025e-01 4.3228848162952316e-01
10.2. Large Softening
|gravity> ruby rknbody9b_driver.rb < cube1.in
eps = 0.1
dt = 0.001
dt_dia = 2
dt_out = 2
dt_end = 2
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2, after 2000 steps :
E_kin = 48.1 , E_pot = -68.8 , E_tot = -20.7
E_tot - E_init = -1e-05
(E_tot - E_init) / E_init = 4.84e-07
8
1.9999999999998905e+00
1.0000000000000000e+00
-2.3357068379703563e+00 -1.5730462500735882e+00 -1.8373515169655967e+00
-3.2503099351457405e+00 -2.2769160097020231e+00 -2.7623089808977994e+00
1.1000000000000001e+00
-1.4462439521294790e+00 -7.9274043868280397e-01 1.9462651835363280e+00
-1.5388550025735492e+00 -8.5033761684692111e-01 2.7987214535075422e+00
1.2000000000000000e+00
-8.4361749490035387e-01 1.8870481468897002e+00 -7.5123041488377962e-01
-5.2602892044713823e-01 2.5585640337825617e+00 -6.5671580935516860e-01
1.3000000000000000e+00
1.6304345239074072e-01 5.8421169904952219e-01 4.1153090918721674e-01
1.3842631574595166e+00 -5.2283176060070413e-01 -5.2052114949956041e-01
1.3999999999999999e+00
3.0263433758971969e-01 -1.2126952329091388e-01 5.4757741932432893e-02
-2.2026773446067907e+00 -1.0870392845510134e-01 -2.4523203993014261e-01
1.5000000000000000e+00
5.7619765613623819e-01 -1.4294804330220603e-01 -9.1132984353013688e-02
-1.0609857121621187e+00 -1.6441584074724240e+00 -9.9518893248749163e-01
1.6000000000000001e+00
5.5584843594067390e-01 -3.6360342031389209e-01 -2.0891409427520066e-01
2.3016236123480418e+00 1.1615617212579910e+00 -5.4794699774267885e-01
1.7000000000000000e+00
5.5859860985306420e-01 -2.4288669549678879e-01 3.3674893916023442e-02
2.8043365345598055e+00 9.3036246676969148e-01 2.2713384109628652e+00
Alice: Great! Very well behaved. And indeed most particles have
just passed through the center, as is clear from their position
components, and are continuing to move on, as their velocity
components indicate.
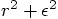 , we have to check
the difference between
, we have to check
the difference between 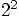 and
and 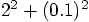 .
The latter is only a quarter of a percent larger than the former. And
for most particle pairs the difference is much smaller still, so the
total difference is likely to be more like a tenth of a percent, too
small to show up within the accuracy with which we print out the energy.
.
The latter is only a quarter of a percent larger than the former. And
for most particle pairs the difference is much smaller still, so the
total difference is likely to be more like a tenth of a percent, too
small to show up within the accuracy with which we print out the energy.
10.3. Even larger softening
|gravity> ruby rknbody9c_driver.rb < cube1.in
eps = 0.3
dt = 0.001
dt_dia = 2
dt_out = 2
dt_end = 2
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.6 , E_tot = -20.6
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2, after 2000 steps :
E_kin = 19.9 , E_pot = -40.5 , E_tot = -20.6
E_tot - E_init = -6.68e-09
(E_tot - E_init) / E_init = 3.25e-10
8
1.9999999999998905e+00
1.0000000000000000e+00
-1.3435332524361765e+00 -1.3215614066272325e+00 -1.3349638266570156e+00
-1.6912633178958605e+00 -1.8593451296223482e+00 -1.9880447778358679e+00
1.1000000000000001e+00
-1.1428786019621284e+00 -1.1455131430342225e+00 1.2256328116240207e+00
-1.1933788723000605e+00 -1.3945830515013942e+00 1.8622141170854261e+00
1.2000000000000000e+00
-9.2565210028918554e-01 1.0727125108268556e+00 -9.6980727607605521e-01
-6.6075234951751749e-01 1.5546315810261460e+00 -1.0191929255321155e+00
1.3000000000000000e+00
-6.7586116933868967e-01 8.5050524262812943e-01 8.0855082812733969e-01
-5.1962467791243423e-02 1.0021841594452070e+00 7.8942187688433141e-01
1.3999999999999999e+00
7.4446049432842354e-01 -4.9008095056780804e-01 -5.0941448582820292e-01
8.6641095431182236e-01 4.6983803735978924e-01 3.8723066728293609e-01
1.5000000000000000e+00
5.2586784274845078e-01 -1.9076507421867578e-01 3.0256970789252191e-01
3.7062049124660296e-01 1.3593990088399948e+00 -9.4199154209711755e-01
1.6000000000000001e+00
3.4351961512732321e-01 1.1579367694820625e-01 8.9914604762325170e-02
2.1678167378492888e-01 -1.3136771019591300e+00 1.4926999954472413e+00
1.7000000000000000e+00
3.5848465570332533e-01 1.0335593797758784e-01 -1.0889250629570488e-01
1.0286337376548356e+00 -2.1764660039138783e-01 -8.1239017296188831e-01
Alice: Good! I'm glad to see that.