9. Softening
Alice: I'm very glad to see that we can integrate eight bodies
in a cold collapse system. This is quite a bit more demanding than
integrating a handful of bodies in a virialized system. However, in
both cases, sooner or later there will be close encounters between
two or more of the particles. Our code will never be able to handle
all of those close encounters. No matter how small a time step we
give it, sooner or later there will be particles that approach each
other closely enough to have a near miss that takes less time than the
time step size. This will necessarily lead to large numerical errors.
Bob: This is of course why people have introduced variable time
steps, as well as a whole order set of algorithmic tools to tame the
unruly behavior of particles that get too close to the inverse square
singularities of Newtonian gravity.
Alice: Soon we will introduce those extensions in our codes,
but for now, there are more urgent things on our agenda. I guess we
just have to live with it, and make sure the students realize that
this first N-body tool is not to be trusted under all circumstances.
Bob: Hmm. I don't much like the idea of giving someone a tool that cannot
be trusted. How about adding softening, as an option?
Alice: You mean to soften the potential, from an inverse square law to
a form that remains finite in the center?
Bob: Indeed. We start from the singular Newtonian potential
energy between two particles with positions
Alice: Yes, this is what is often used in collisionless stellar dynamics,
to suppress the effect of close encounters. I can't say I'm very happy
with this softening approach, since it's not the real thing. It is purely
a mathematical trick, to avoid numerical problems.
Bob: Well, you can give it a physical interpretation. Instead of using
point particles, which are not very physical in the first place, each particle
gets a more extended mass distribution. In fact, you can easily show that
a softened potential corresponds to a mass distribution given by a polytrope
of index five, better known as a Plummer mass distribution:
Bob: It would be quite easy to use a different mass distribution,
corresponding a finite support. This is what people so who work with
SPH particles, for example. However, for or current purpose, the main
thing is to provide a tool that works, and we can worry later about
aesthetic details.
Alice: Okay. Even though I can't say I'm very happy with it, I see
your point, and it is certainly safer to give the students a tool that
is guaranteed to give finite answer.
Bob: It should be easy to add softening to our code. Time to create
another version for our N-body code! So we will call this new file
rknbody9.rb. Well, this will take me a while.
Alice: Okay, I'm way behind in reading the astro-ph abstracts. This
will give me a chance to catch up. I'll come back when I've gone through
them.
Bob: Here it is, the new version of our N-body code, now with softening
build in. It was quite straightforward to make the changes. First of all,
here is the new driver:
As you can see, minimal differences, contained in three lines. The
method evolve has an extra parameter, eps, the softening length.
The default value is zero, which means no softening at all. The third
new line is where the value of eps is echoed on the standard error
stream.
Alice: So now evolve has eight parameters. At some point we may
want to think about grouping them together, perhaps creating a class
for them, since there is clear substructure: two flags controlling the
amount of output, three variables giving intervals between output times,
and three other variables.
Bob: But not now.
Alice: Not now, no. Can you show me the code itself?
Bob: Here it is. Almost all changes speak for themselves.
Alice: Even though the changes may speak for themselves, I have some
questions. First of all, the value of eps has to be passed on
from the driver, where it is defined, through evolve into Nbody
and then down to the methods within Body that do all the hard work.
Bob: First of all, I gave the Nbody class an extra instance variable,
@eps, which stores the value of the softening. As soon as evolve
is executed, within the Nbody class, the first thing it does is assign
the proper value to @eps, as well as to @dt, as was done
already in our previous version:
Alice: I see. In that way, you don't have to give an extra argument
to the integration methods, for example: they can just pick up the value
of the softening length from @eps, to which they have automatic
access, as Nbody class methods. But of course they do have to
pass that value down to the particles, which are realized as instances
of the Body class, since otherwise the particles would not know what
softening to use.
Bob: The one thing I didn't like very much is that the lines in the
integration methods have become somewhat longer. Forward Euler,
for example, has grown now from:
to:
I'm not too happy with the fact that acc now has to get a second
argument. But that's the way it is.
If I really would want to make the lines shorter, I could
use shorter variables than ba and eps, for example a and e.
But let us not spend more time on such niceties, which give us
diminishing return in clarity at the cost of making the code more
complex and hence less clear.
Alice: I fully agree. Instead, let's see how your new code performance
in our cold collapse experiment. 9.1. Close Encounters
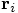 and
and
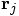 and masses
and masses 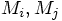 :
:

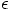 :
:
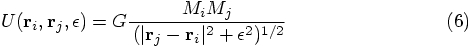
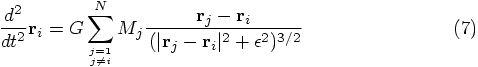
 , this
last equation again returns to the Newtonian gravitational acceleration.
, this
last equation again returns to the Newtonian gravitational acceleration.
9.2. Fuzzy-Point Particles

 . You solution works, in
the sense of avoiding singularities, and it gives a roughly reasonable answer,
but it does come at the cost of smearing each particle all over space.
. You solution works, in
the sense of avoiding singularities, and it gives a roughly reasonable answer,
but it does come at the cost of smearing each particle all over space.
9.3. A New Driver
9.4. A Code with Softening
9.5. Details
def forward
calc(" @old_acc = acc(ba) ")
calc(" @pos += @vel*dt ")
calc(" @vel += @old_acc*dt ")
end