8. An Eight-Body System
Bob: Now that we have settled on a tool for doing N-body simulations,
it would be a pity to stop with three bodies. Let's try it out on a
bunch more particles.
Alice: We haven't yet written tools for setting up initial conditions,
though, such as a Plummer model, or a King model, or even just a
homogeneous sphere with particles sprinkled in. We will certainly do
that later, but starting with that right know would be too much of a
distraction. After all, it was you who wanted to move on quickly to
graphics!
Bob: I agree. Let's do something really simple then. How about
setting up eight particles on the eight corners of a cube, centered on
the origin? We can start with all particles at rest, and just let
them fall toward each other.
Alice: That sounds like a reasonably quick try. But we cannot give
them equal masses, otherwise by symmetry they will all hit each other
in the center, at distance zero from each other, where the inter-particle
forces will be infinitely large.
Bob: Yes, we have to perturb something. Either we can give them
equal masses, and small but different initial velocities, or we can
give them zero velocities but slightly different masses. Let me do
the latter. Here are some initial conditions:
Alice: The advantage of perturbing the masses, rather than the velocities,
is that you keep the center of mass at rest. In other words, the kinetic
energy you will be measuring, as soon as the particles start moving, will
be the energy of the internal motion only. It will not receive a contribution
from the kinetic energy associated with center-of-mass motion. If you had
perturbed the velocities arbitrarily, that would no longer be true.
Bob: Let's guess how long would it take for the particles to reach
the center. The masses are of order unity, the distances also, so the
accelerations must also be of order unity. This would suggest that it
would take of order one time unit for the particles to meet each other.
Well, let us ask the computer to tell us whether it will take them
more than one time unit or less.
Alice: Hmm, we should be able to predict that before doing a run.
Wasn't it John Wheeler, who told us never to do a calculation before
you know the answer? I like his attitude. Relying too much on raw
computer power can make you lazy.
Bob: Lazy is in the eye of the beholder, I guess: it is a lot of
work to write a good computer program, as we both know! But I see your
point. It certainly doesn't hurt to try to predict numerical results
beforehand, and it makes you more likely to catch a bug, if things
come out differently from what you expected.
Alice: Not only that, it will give you more physical insight into the
answer as well.
Bob: Okay, let's see whether we can predict the outcome of our
particle race toward the center. I started saying that inter-particle
distances were of order unity. However, the typical distances between
particles are actually more like 2, 3 or 3.5, roughly speaking as an
approximation for
Now this means that when you start from rest, and you have a distance
to the center of
Alice: I agree. Okay, we have placed our bets. Let the truth be
revealed! And actually, this would be a good time to use the x_flag
that we built in to ask for extra information about accelerations.
Bob: Good idea. Okay, here goes, let's run things for one time unit:
Alice: And indeed, the particles did not reach the center yet.
The first particle, for example, that started at the right-far-upper
corner, at
Bob: And look, my guestimate for the accelerations was correct too.
Going back to the first snapshot output, typical components for the
acceleration at time zero are 0.6 and 0.7, which means in three
dimensions that the magnitude of the acceleration vector must be
something like
Alice: Yes, well done! And our integrator has behaved well, too,
even with the rather large time step of 0.1 that we have given it.
Perhaps this is not surprising, given that the particles haven't reached
the central crunch yet.
Bob: I bet things won't go so well for the next time unit. But
let's try and see what happens:
Alice: A veritable numerical explosion! Look, the total energy has
changed from a negative value around -20 to an enormously large
positive value. So much for energy conservation. Clearly we'll have
to try a much smaller time step.
Bob: At least the particles have passed through the center, as you
can see from the particles that reversed the signs of the values of
the components of their position vectors -- although some of the particles
seem to have gone of in almost random directions, with great speed.
Okay, let's make the time step a hundred times smaller. We did start
off with a rather unrealistically large time step value, after all.
Alice: And let's cut down on the output for now, showing only the
energy errors for a few runs. If we give a large value, say 10, for
the snapshot output interval, no snapshot will appear during our run.
Here we go again:
8.1. Setting Up a Cube
8
0
1.0
1 1 1
0 0 0
1.1
1 1 -1
0 0 0
1.2
1 -1 1
0 0 0
1.3
1 -1 -1
0 0 0
1.4
-1 1 1
0 0 0
1.5
-1 1 -1
0 0 0
1.6
-1 -1 1
0 0 0
1.7
-1 -1 -1
0 0 0
As you can see, I took masses starting from 1.0 with increments of 0.1
for each next particle as I was walking around the eight corners of the
central cube, for which the edges all have a length of 2.
8.2. Letting Go
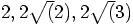 , depending
whether they share an edge, a side, or nothing at all. So the initial
acceleration, with inverse square forces, will receive contributions
that have a distance dependence of something like
, depending
whether they share an edge, a side, or nothing at all. So the initial
acceleration, with inverse square forces, will receive contributions
that have a distance dependence of something like
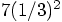 , if we take 3 as a typical distance. With a
typical mass being somewhat larger than 1, we do indeed get an
acceleration that is fairly close to 1, between 0.75 and 1.5, I would
guess.
, if we take 3 as a typical distance. With a
typical mass being somewhat larger than 1, we do indeed get an
acceleration that is fairly close to 1, between 0.75 and 1.5, I would
guess.
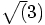 or roughly 1.7, it will take
more than one time unit to arrive at the center. Of course, nonlinear
effects will complicate things, but I don't think they will invalidate
this simple reasoning so quickly. I'm pretty sure that by time
t = 1, the particles haven't arrived in the center yet.
or roughly 1.7, it will take
more than one time unit to arrive at the center. Of course, nonlinear
effects will complicate things, but I don't think they will invalidate
this simple reasoning so quickly. I'm pretty sure that by time
t = 1, the particles haven't arrived in the center yet.
|gravity> ruby rknbody8b_driver.rb < cube1.in
dt = 0.1
dt_dia = 1
dt_out = 10
dt_end = 1
init_out = false
x_flag = true
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
for debugging purposes, here is the internal data representation:
mass = 1.0
pos = 1.0, 1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = -0.705795165844984, -0.63811749631532, -0.604278661550489
mass = 1.1
pos = 1.0, 1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = -0.725983913601737, -0.658306244072073, 0.556789739777578
mass = 1.2
pos = 1.0, -1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = -0.74617266135849, 0.543139652769499, -0.644656157063995
mass = 1.3
pos = 1.0, -1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = -0.766361409115244, 0.563328400526252, 0.597167235291084
mass = 1.4
pos = -1.0, 1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = 0.515839478753342, -0.718872487342333, -0.685033652577501
mass = 1.5
pos = -1.0, 1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = 0.536028226510095, -0.739061235099086, 0.637544730804591
mass = 1.6
pos = -1.0, -1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = 0.556216974266848, 0.623894643796512, -0.725411148091007
mass = 1.7
pos = -1.0, -1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = 0.576405722023601, 0.644083391553265, 0.677922226318097
at time t = 1, after 10 steps :
E_kin = 12.3 , E_pot = -33 , E_tot = -20.7
E_tot - E_init = 0.000633
(E_tot - E_init) / E_init = -3.05e-05
for debugging purposes, here is the internal data representation:
mass = 1.0
pos = 0.597644451816504, 0.63640287626745, 0.655762419276459
vel = -0.940991555344834, -0.850014228000948, -0.80458017381832
acc = -1.71506911283474, -1.54866562852442, -1.4652605274951
mass = 1.1
pos = 0.585134269661813, 0.624094692341221, -0.682431788577738
vel = -0.973577364186811, -0.881473975864098, 0.743630411318128
acc = -1.79677056984513, -1.62409268319797, 1.36430528840404
mass = 1.2
pos = 0.572566955655305, -0.689897591000862, 0.631297823877706
vel = -1.00651894751619, 0.727233325183985, -0.866662302150037
acc = -1.88087240679652, 1.34171513605627, -1.6115608160994
mass = 1.3
pos = 0.559940111130521, -0.677904296108633, -0.658282111563603
vel = -1.03983780651743, 0.756905613895535, 0.803924789872002
acc = -1.96757353300315, 1.40685742201327, 1.50031839892619
mass = 1.4
pos = -0.705282791726003, 0.586860755993474, 0.60663858079331
vel = 0.69165870948931, -0.977682574453683, -0.92985560640001
acc = 1.27847519172173, -1.86192287793191, -1.76451307558405
mass = 1.5
pos = -0.693423631896722, 0.574338867566358, -0.633959293898993
vel = 0.720463619202033, -1.01042621662886, 0.86512158769774
acc = 1.33750716238934, -1.94561109813966, 1.64085701293565
mass = 1.6
pos = -0.681529221962402, -0.64167993353146, 0.581767543659952
vel = 0.749410199081073, 0.847120045366664, -0.99430431139073
acc = 1.39673308307382, 1.60737124811481, -1.92531904373592
mass = 1.7
pos = -0.669597957823065, -0.629517535170942, -0.609447786811517
vel = 0.778508588720364, 0.877635982210738, 0.927342131031408
acc = 1.45618251518339, 1.67618202793406, 1.78678060432799
N = 8
time = 0.0
N = 8
time = 1.0
8.3. Passing Through
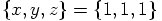 still has positive values
for all three position components, and velocity components that are
all negative, indicating that it is moving toward the center, but hasn't
quite gotten there yet. It is about half way, judging from the size
of the position components.
still has positive values
for all three position components, and velocity components that are
all negative, indicating that it is moving toward the center, but hasn't
quite gotten there yet. It is about half way, judging from the size
of the position components.
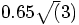 , say, or about 1.1; comfortable
within my predicted range!
, say, or about 1.1; comfortable
within my predicted range!
|gravity> ruby rknbody8c_driver.rb < cube1.in
dt = 0.1
dt_dia = 2
dt_out = 10
dt_end = 2
init_out = false
x_flag = true
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
for debugging purposes, here is the internal data representation:
mass = 1.0
pos = 1.0, 1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = -0.705795165844984, -0.63811749631532, -0.604278661550489
mass = 1.1
pos = 1.0, 1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = -0.725983913601737, -0.658306244072073, 0.556789739777578
mass = 1.2
pos = 1.0, -1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = -0.74617266135849, 0.543139652769499, -0.644656157063995
mass = 1.3
pos = 1.0, -1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = -0.766361409115244, 0.563328400526252, 0.597167235291084
mass = 1.4
pos = -1.0, 1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = 0.515839478753342, -0.718872487342333, -0.685033652577501
mass = 1.5
pos = -1.0, 1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = 0.536028226510095, -0.739061235099086, 0.637544730804591
mass = 1.6
pos = -1.0, -1.0, 1.0
vel = 0.0, 0.0, 0.0
acc = 0.556216974266848, 0.623894643796512, -0.725411148091007
mass = 1.7
pos = -1.0, -1.0, -1.0
vel = 0.0, 0.0, 0.0
acc = 0.576405722023601, 0.644083391553265, 0.677922226318097
at time t = 2, after 20 steps :
E_kin = 1.58e+03 , E_pot = -4.79 , E_tot = 1.57e+03
E_tot - E_init = 1.6e+03
(E_tot - E_init) / E_init = -76.9
for debugging purposes, here is the internal data representation:
mass = 1.0
pos = -3.02971661137991, -2.24193089826656, -2.25919153274194
vel = -4.87425095159097, -3.66549478896126, -3.74246308641192
acc = 0.0606083601111188, 0.0515883922084716, 0.0733897970440225
mass = 1.1
pos = -4.31240799333488, -3.10616175910087, 3.14764781958622
vel = -6.86534163590612, -5.02388641613739, 5.35062470064063
acc = 0.0615581909052363, 0.0415529106299662, -0.0445228494603485
mass = 1.2
pos = -1.62568960640959, 3.34494098204815, -1.6622442836446
vel = -2.3870995554365, 5.56374518497225, -2.53222993754156
acc = 0.00462833018233916, -0.139148363026155, 0.101906470797269
mass = 1.3
pos = -1.50564040892264, 1.27774837383927, 0.881834075119233
vel = -2.08881245118275, 2.16684233579503, 1.29915422585319
acc = -0.0179375991256231, -0.0112123628543447, -0.0971526926290998
mass = 1.4
pos = 2.32076951856892, -4.11004315117335, -4.08236760983636
vel = 3.97924211487247, -6.25425810387294, -6.25833469237557
acc = -0.0488286812931284, 0.0362709826406403, 0.0495677416334056
mass = 1.5
pos = 2.94056101577017, -5.90875150100682, 5.68060097022845
vel = 4.91294310127069, -8.99490408184316, 8.88351464915947
acc = -0.0382215840668386, 0.0318234057191825, -0.0300100124207618
mass = 1.6
pos = 6.9881569489367, 11.4122398477483, -16.2293505526342
vel = 11.1558374351108, 17.787395714252, -24.9415505085132
acc = -0.00580613947864572, -0.00923780971388437, 0.0119874756627306
mass = 1.7
pos = -5.15261441447721, -2.6227584261269, 13.1802716803286
vel = -7.5197594733857, -3.83125593317898, 20.3231933860916
acc = 0.0143675680082912, 0.000307955710085254, -0.0376257105250154
N = 8
time = 0.0
N = 8
time = 2.0
8.4. Convergence
|gravity> ruby rknbody8d_driver.rb < cube1.in
dt = 0.001
dt_dia = 2
dt_out = 10
dt_end = 2
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2, after 2000 steps :
E_kin = 2.35e+03 , E_pot = -7.15 , E_tot = 2.35e+03
E_tot - E_init = 2.37e+03
(E_tot - E_init) / E_init = -114
Bob: Still a disaster. Well, these particle energy errors have
little meaning, of course, once they are larger than the original
energy values. So we have no way of knowing how much smaller we'll
have to make the time step. Let's just try a time step value that is
a factor ten smaller.
|gravity> ruby rknbody8e_driver.rb < cube1.in
dt = 0.0001
dt_dia = 2
dt_out = 10
dt_end = 2
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2, after 20000 steps :
E_kin = 65.3 , E_pot = -86.1 , E_tot = -20.7
E_tot - E_init = -0.00705
(E_tot - E_init) / E_init = 0.00034
Alice: Much better already! It seems that we're finally converging.
But I'd like to be sure. How about a time step that is smaller yet,
by a factor two:
|gravity> ruby rknbody8f_driver.rb < cube1.in
dt = 5.0e-05
dt_dia = 2
dt_out = 10
dt_end = 2
init_out = false
x_flag = false
method = rk4
at time t = 0, after 0 steps :
E_kin = 0 , E_pot = -20.7 , E_tot = -20.7
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 2, after 40000 steps :
E_kin = 76.7 , E_pot = -97.5 , E_tot = -20.7
E_tot - E_init = -0.000228
(E_tot - E_init) / E_init = 1.1e-05
Bob: Convergence declared. Good! Normally, a fourth-order
integrator should get a factor 16 more accurate when you half the
time step, so this is very satisfactory.