4. Debugging the N-body Code
Bob: Okay, ready to chase and catch our bug?
Alice: Sure thing! And I like your idea to simplify things and turn
to our old friend, the forward Euler algorithm. And we may as well
make the total integration time a bit shorter, to speed things up.
Alice: Okay, this is really wrong. Almost the same magnitude for the
error.
Bob: Now that we know that the forward Euler method also fails for this
orbit, we can take a single time step, and track things by hand.
The y components of the positions should be equal to
As for the velocities, their y components should be unchanged,
and indeed that is the case.
Finally, the x components of the velocities should be equal to
Alice: Yes, it is much easier to visually inspect a forward Euler scheme
than a fourth-order Runge-Kutta, I agree!
Bob: But how strange. It seems that there is really nothing wrong with
this step. If this step is correct, how can things go wrong later on?
Admittedly, we are still starting from a somewhat special case, launching
our particles parallel to the y axis, while being positioned on the
x axis. Perhaps we should take a really generic initial position,
not lined up with anything at all?
Alice: Hmmm. You know, it might indeed be that the integration is
proceeding fine, but that there is an error in the determination of
the energy error.
Bob: Ah, that could well be the case. That would be like trying to land
an airplane, and to see a warning light coming on, telling you that
your landing gear is not fully unfolded. There are two possibilities:
either your landing gear is faulty or the warning light is
malfunctioning.
Alice: If I were the pilot, I would surely hope that it is the warning light
that is at fault. In our case either way is no problem, either way, as long
as we can trace where what went wrong.
Bob: But for tracking down energy diagnostics, we really have to get back
to the code, and read all the lines that compute energies. Unlike the
integration itself, where we can slow down to take just one time step,
the energy diagnostics have no free parameter; either you do it or you don't.
Alice: Before we look at the code, let us stare at the output just a bit
longer. It still may give us a clue. But I don't like to think about
slightly eccentric and slightly non-unity masses. Let us run the equal-mass
circular binary with masses unity once more, and that one, too, for just one
time step:
Alice: I guess we'll have to walk through the code, much as I don't like
to do that, as a matter of principle. A good code should give you
enough diagnostics to allow you to track down a bug by treating it as
a black box.
Bob: The only other numbers here, apart from the energy errors, are the
kinetic and potential energy, and they are obviously correct, given the
values for the circular binary: at distance 1 and masses 1, the potential
energy must be -1, and with velocity 0.5, each kinetic energy is 1/4,
so 0.5 in total.
Alice: Ah, you are looking at the energies at time t = 0.
That is a great idea: if it is a matter of the warning light malfunctioning,
chances are that it already malfunctioned when the plane took off!
Bob: But I've just shown that it did not malfunction!
Alice: But the circular binary did not give us any problems. It was the
non-unity masses and the eccentricity that did it. Let us redo that one
forward Euler step, which showed a correct integration in that case,
and let us check by hand whether the initial energy is computed
correctly there. Let us put everything on the table once more. First
the initial conditions:
Bob: So it is the warning light, after all. The potential energy gets
calculated correctly, but the kinetic energy doesn't. That will be easy
to check. Here is the method in the Body class:
And indeed, I left out the mass! How simple. Of course, it should have
been:
And I can understand now why I made that mistake: in our earlier two-body
code the corresponding method was:
and as the comment indicated, there it was defined per unit of
reduced mass. I just erased the comment, since I knew that the
concept of reduced mass only applies to a two-body problem, and not to
the general N-body problem. But although I erased the comment, I
failed to change the code line itself, by adding the mass factor!
What a blunder. And I even commented on the fact that I was so careful
to include an extra mass factor in my definition of the potential energy!
But in that case, I was modeling the potential energy method epot
after the method acc that calculates the acceleration, because both
involve a loop over all other particles. That is why I did not
compare the epot and ekin methods.
Alice: Well, it is an easy mistake to make. I have made plenty of
much more obvious mistakes in my life! The challenge is not so much
to write correct code, but to debug code correctly. And I think we
did pretty well, given the fact that this was a very tricky bug to
discover in the first place.
Bob: Tricky indeed: if we would have only tried a circular orbit, even
with masses that were not unity, we would have never found this bug.
I'm very glad now that you insisted on using unequal masses!
Alice: Unequal masses and eccentricity. If we would have used unequal
masses for an eccentric orbit, we still would not have seen a
problem with energy conservation. The energy would have been
calculated wrong at time t=0, but for a circular orbit,
energy and potential remain constant throughout the orbit. So the
same mistake in kinetic energy would have been present at any later
time, and the code would have reported no significant energy change;
our energy drift warning light would not have come on!
Bob: You are right. Now that is a tricky bug. Clearly the moral of the
story is: test any new code for generic input data, not only for input data
that are easy to generate and easy to interpret.
Alice: Ah, but wait a minute! Before we congratulate ourselves too much,
I wonder whether we should not have noticed that there was something wrong
with the energies in the case of the circular orbit where the masses
of the two stars were equal to each other, but different from unity. Let
us look at that case again. Where did we file those data? Ah, here it is:
we stored the initial conditions in the file test3.in:
Alice: We should have, yes, but we didn't. It goes to show: even with
good diagnostics, it is easy to overlook a trouble signal. To
continue with your analogy of a pilot, looking at a warning signal: in
a cockpit with many different indicators, one can overlook the fact
that one of the meters gives an impossible result. We were staring at
the red light of errors in energy conservation, and we overlooked the
less obvious lights.
Bob: Still, I feel pretty stupid that I didn't see that we were setting
up a binary with binding energy of the wrong sign.
Alice: Well, that makes two of us. But the goal of good software
development is not to make programmers perfect, since that is impossible.
Instead, the goal should be to make debugging easy enough, so that
imperfect people can still converge to an almost-perfect code, when
they try hard enough. This in itself is already enough of a reason
for using a language like Ruby, where the programmers are not bogged
down with trying to keep the compiler happy. We can at least spend
all of our energy on the debugging process itself, without worrying
about declarations and type checking and all the other constraints
that the more classical languages always bring with them.
Bob: You have a charitable interpretation of human weakness. Even so,
I really will try not to make this kind of silly mistake again.
Alice: Famous last words!
Bob: So, we're done!
Alice: It seems that way. But it would not hurt to test our
original run again, now that you have fixed the code. You know, it
would not be the first time that a code contains more than one bug.
Another common mistake people make is to find a glaring bug in a code,
fix it, and then happily declare the code to be correct, without
looking further.
Bob: Okay! I will call the corrected version rknbody2.rb, since
I would like to keep the original file rknbody1.rb, to show
to my students later on. It would be interesting to see how they
would go about debugging it. Here is our original run, but now with
the corrected code:
Alice: That's it: the energy conservation is perfect. But let us not
declare victory too early: let's compare the actual positions and velocities
with what we got with our earlier two-body code. However, to compare
the data, it would be better to convert our results to relative coordinates
between the two particles. That should be easy: let us make a little script
for this simple form of data reduction, and call it
rknbody2a_reduce.rb:
All it does is to read in an N-body system, and print the relative positions
and velocities of the first two particles with respect to each other.
We can then pipe the results from our previous calculation into our
new script:
Alice: For the time being, yes. But I would never discount the possibility
that somewhere, in some dark corner, some other little bug may still be hiding.
However, at some point you just have to move on, while staying
vigilant, always being prepared to go back to inspect older codes that
you were convinced to be fully debugged.
Bob: By the way, I'm glad we decided to put the energy diagnostics on the
standard error stream STDERR, while keeping only the particle output
on the standard output stream. If we would have written everything on
the standard output, it would have been impossible to pipe the data
into the next program, as we did above.
Alice: For now, yes, that was a good strategy. But I worry about the
idea of scattering related data in completely different directions.
Actually, it would be even better to encapsulate the error diagnostics
somewhere in the output, in order to keep the data together. Soon we
should introduce a new data format, once that keeps everything bundled,
but in such a way that the next program will have a fixed and known way
to find the data it wants.
Bob: You mean a form of self-describing data? Like the FITS format that
observers use? Yes, that would be interesting, and it would not be too hard
to implement. 4.1. Forward Euler
|gravity> ruby rknbody1c_driver.rb < test5.in
dt = 0.0001
dt_dia = 1
dt_out = 1
dt_end = 1
method = forward
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 10000 steps :
E_kin = 0.875 , E_pot = -1.37 , E_tot = -0.497
E_tot - E_init = 0.0628
(E_tot - E_init) / E_init = -0.112
2
9.9999999999990619e-01
9.0000000000000002e-01
3.8764717723091237e-02 2.9255040141287891e-01
-8.9213055091367810e-01 -2.8150072109002572e-01
9.0000000000000002e-01
-3.8764717723091237e-02 -2.9255040141287891e-01
8.9213055091367810e-01 2.8150072109002572e-01
Bob: That doesn't look too good, but then again, forward Euler is not a
great integrator. I'll give it a ten times smaller time step:
|gravity> ruby rknbody1d_driver.rb < test5.in
dt = 1.0e-05
dt_dia = 1
dt_out = 1
dt_end = 1
method = forward
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 1, after 100000 steps :
E_kin = 0.876 , E_pot = -1.37 , E_tot = -0.497
E_tot - E_init = 0.0626
(E_tot - E_init) / E_init = -0.112
2
9.9999999999808376e-01
9.0000000000000002e-01
3.8685902921474627e-02 2.9243384480372231e-01
-8.9221956236710909e-01 -2.8194011853141043e-01
9.0000000000000002e-01
-3.8685902921474627e-02 -2.9243384480372231e-01
8.9221956236710909e-01 2.8194011853141043e-01
4.2. Nothing Wrong
|gravity> ruby rknbody1e_driver.rb < test5.in
dt = 0.01
dt_dia = 0.01
dt_out = 0.01
dt_end = 0.01
method = forward
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.01, after 1 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0.000121
(E_tot - E_init) / E_init = -0.000217
2
1.0000000000000000e-02
9.0000000000000002e-01
5.0000000000000000e-01 5.0000000000000001e-03
-9.0000000000000011e-03 5.0000000000000000e-01
9.0000000000000002e-01
-5.0000000000000000e-01 -5.0000000000000001e-03
9.0000000000000011e-03 -5.0000000000000000e-01
Let me print out the initial conditions again:
2
0
0.9
0.5 0
0 0.5
0.9
-0.5 0
0 -0.5
The initial velocity is along the y axis, so after one step the x
components of the positions of the particles should not be affected.
Indeed, they remain at 0.5.
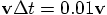. And so they are.
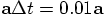. The acceleration, for particles of
mass 0.9, at distance 1, should be 0.9, which means that 
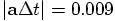. All that checks too.
4.3. Two Possibilities
|gravity> ruby rknbody1e_driver.rb < test2.in
dt = 0.01
dt_dia = 0.01
dt_out = 0.01
dt_end = 0.01
method = forward
at time t = 0, after 0 steps :
E_kin = 0.5 , E_pot = -1 , E_tot = -0.5
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.01, after 1 steps :
E_kin = 0.5 , E_pot = -1 , E_tot = -0.5
E_tot - E_init = 0.0002
(E_tot - E_init) / E_init = -0.0004
2
1.0000000000000000e-02
1.0000000000000000e+00
5.0000000000000000e-01 7.0710678118654745e-03
-1.0000000000000000e-02 7.0710678118654746e-01
1.0000000000000000e+00
-5.0000000000000000e-01 -7.0710678118654745e-03
1.0000000000000000e-02 -7.0710678118654746e-01
Bob: This one, too, is perfect. I'm getting better at `reading' the
forward Euler output: I can see now immediately that both the directions
and the magnitudes of the increments in position and velocity are correct.
The acceleration here is just 1.
4.4. Back to Square One
2
0
0.9
0.5 0
0 0.5
0.9
-0.5 0
0 -0.5
Then the result of the one time step:
|gravity> ruby rknbody1e_driver.rb < test5.in
dt = 0.01
dt_dia = 0.01
dt_out = 0.01
dt_end = 0.01
method = forward
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 0.01, after 1 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0.000121
(E_tot - E_init) / E_init = -0.000217
2
1.0000000000000000e-02
9.0000000000000002e-01
5.0000000000000000e-01 5.0000000000000001e-03
-9.0000000000000011e-03 5.0000000000000000e-01
9.0000000000000002e-01
-5.0000000000000000e-01 -5.0000000000000001e-03
9.0000000000000011e-03 -5.0000000000000000e-01
The initial potential energy must be equal to the square of the masses,
divided by the distance,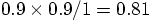 
. That
is indeed what the code gives. The initial kinetic energy for each
particle must be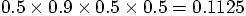 
,
so for both particles together 
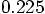. Hey! The code output
gives us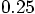 
!
4.5. A Warning Light
def ekin # kinetic energy
0.5*(@vel*@vel)
end
def ekin # kinetic energy
0.5*@mass*(@vel*@vel)
end
def ekin # kinetic energy
0.5*(@vel*@vel) # per unit of reduced mass
end
4.6. Hindsight
2
0
0.1
0.5 0
0 0.22360679774997896964
0.1
-0.5 0
0 -0.22360679774997896964
Let us run that case again, with the original code rknbody1.rb:
|gravity> ruby rknbody1a_driver.rb < test3.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.05 , E_pot = -0.01 , E_tot = 0.04
E_tot - E_init = 0
(E_tot - E_init) / E_init = 0
at time t = 10, after 100000 steps :
E_kin = 0.05 , E_pot = -0.01 , E_tot = 0.04
E_tot - E_init = -2.64e-15
(E_tot - E_init) / E_init = -6.59e-14
2
9.9999999999900329e+00
1.0000000000000001e-01
-1.1897419599036606e-01 -4.8563889948034655e-01
2.1718431835122404e-01 -5.3206877960568291e-02
1.0000000000000001e-01
1.1897419599036606e-01 4.8563889948034655e-01
-2.1718431835122404e-01 5.3206877960568291e-02
Bob: You are right! Now that we know what to look for, it is obvious
that the diagnostics output is totally wrong. Already at time t = 0,
the total energy is positive: E_tot = 0.04. A binary with positive
total energy will immediately fly apart. We should have noticed that right
away!
4.7. Bug Fixed
|gravity> ruby rknbody2a_driver.rb < test1.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.02 , E_pot = -0.16 , E_tot = -0.14
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.0887 , E_pot = -0.229 , E_tot = -0.14
E_tot - E_init = 4.55e-15
(E_tot - E_init) / E_init = -3.25e-14
2
9.9999999999900329e+00
8.0000000000000004e-01
1.1992351097726084e-01 -7.2126916688572407e-02
2.0616138205436191e-01 4.2779060839347856e-02
2.0000000000000001e-01
-4.7969404390904336e-01 2.8850766675428963e-01
-8.2464552821744763e-01 -1.7111624335739142e-01
4.8. One More Check
|gravity> ruby rknbody2a_driver.rb < test1.in | ruby rknbody2a_reduce.rb
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.02 , E_pot = -0.16 , E_tot = -0.14
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.0887 , E_pot = -0.229 , E_tot = -0.14
E_tot - E_init = 4.55e-15
(E_tot - E_init) / E_init = -3.25e-14
relative_position = [0.599617554886304, -0.360634583442862]
relative_velocity = [1.03080691027181, 0.213895304196739]
And compare the results with what we found directly with our two-body code:
|gravity> ruby integrator_driver2h.rb < euler.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 100000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = -8.33e-14
(E_tot - E_init) / E_init =9.52e-14
1.0000000000000000e+00
5.9961755488723312e-01 -3.6063458344261029e-01
1.0308069102701605e+00 2.1389530419780176e-01
Bob: Indeed, very closely the same, to well over ten decimals! Very nice.
I think we can declare victory now.