3. Testing the N-body Code
Alice: I would like to see the N-body program running for a 2-body system
first, just to check whether we really get the same results.
Bob: That's a good idea. I have tested it so far with a 3-body system,
with some randomly chosen initial conditions, but I agree that it would be
good to test the code from the ground up. Shall we try to reproduce the
same Kepler orbit that we integrated using our euler.in initial
conditions? They were
Bob: Good idea. We saw already how using a mass of unity could fail
to show an error in mass assignment. The more asymmetric and non-default
our choice is, the better. It would be good, though, to calculate the
orbits in the center-of-mass frame, otherwise the results are more
difficult to interpret, when the particles start drifting off, away
from the origin. How about this choice? I'll put it in a file
test1.in:
Here is the result:
Now let's see what my new N-body code, rknbody1a_driver.rb,
will do. Here is the code:
And here is what it does:
Bob: Yes, I'm sure, I can show you. And yes, I'm deeply puzzled now.
Alice: Let's try a very simple situation, where we absolutely know what
the outcome will be, in explicit form. Let us take a circular binary star
with equal masses, just to see what will go wrong there. Perhaps that will
give us a hint. We can give both stars a mass
Bob: Here we go. I will call the initial file for the circular binary
test2.in.
Alice: Congratulations! You do have a working integrator, at least
for a circular equal-mass binary. But of course the question remains:
what went wrong with the non-circular non-equal-mass binary?
Bob: I'm stumped. But this is a bug we should be able to track down
without too much trouble. The last case, which worked, was special in
at least three ways: the orbit was circular, the masses were equal,
and the masses were also all equal to unity. The case which didn't
work did have none of these three idealizations. Let's modify each of
those in turn.
Alice: It may be easiest to drop the unity of the masses. If we make
the mass ten times smaller, the potential energy becomes one hundred times
smaller, and so should the kinetic energy of each particle. Since the mass
is already ten times smaller, we can make the kinetic energy a hundred
times smaller but lowering the velocity by a factor
Bob: Here goes, with test3.in:
Alice: Nothing wrong here. So changing the masses did not help, at least
not for our circular orbit. Shall we try to increase the eccentricity,
while leaving the masses both unity? We can just make the velocities a bit
smaller. How about this, as the file test4.in:
Bob: Still no cigar. Nothing wrong here either. How about changing
both the masses and the eccentricity? I'll just make the masses ten
percent smaller, while leaving everything else the same, calling the
file test5.in:
Bob: We're getting a little closer, but we may still have quite a ways to go!
3.1. A 2-Body System
1
1 0
0 0.5
Alice: Yes, but now we have to be careful how we interpret this mass
value of 1 that we used before. Remember how we introduced the two-body
problem, using the relative position 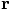 between the two
pairs? The equation of motion for
between the two
pairs? The equation of motion for 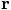 was
was

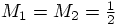 .
However, I would prefer unequal masses, just to avoid degenerate
situations where our test may fail to uncover some subtle bug.
.
However, I would prefer unequal masses, just to avoid degenerate
situations where our test may fail to uncover some subtle bug.
2
0
0.8
0.2 0
0 0.1
0.2
-0.8 0
0 -0.4
I will first redo the fourth-order Runge-Kutta run for a time step
of 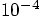 , using our previous two-body code,
integrator_driver2h.rb:
, using our previous two-body code,
integrator_driver2h.rb:
|gravity> ruby integrator_driver2h.rb < euler.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.125 , E_pot = -1 , E_tot = -0.875
E_tot - E_init = 0
(E_tot - E_init) / E_init =-0
at time t = 10, after 100000 steps :
E_kin = 0.554 , E_pot = -1.43 , E_tot = -0.875
E_tot - E_init = -8.33e-14
(E_tot - E_init) / E_init =9.52e-14
1.0000000000000000e+00
5.9961755488723312e-01 -3.6063458344261029e-01
1.0308069102701605e+00 2.1389530419780176e-01
3.2. A Bug
|gravity> ruby rknbody1a_driver.rb < test1.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.085 , E_pot = -0.16 , E_tot = -0.075
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.377 , E_pot = -0.229 , E_tot = 0.148
E_tot - E_init = 0.223
(E_tot - E_init) / E_init = -2.98
2
9.9999999999900329e+00
8.0000000000000004e-01
1.1992351097726084e-01 -7.2126916688572407e-02
2.0616138205436191e-01 4.2779060839347856e-02
2.0000000000000001e-01
-4.7969404390904336e-01 2.8850766675428963e-01
-8.2464552821744763e-01 -1.7111624335739142e-01
Alice: Huh? An energy conservation error of order unity? And our old
code was conserving energy almost on machine accuracy! Are you sure you
have tested your code?
3.3. The Simplest Case
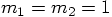 ,
and start with an initial distance of
,
and start with an initial distance of 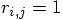 . This
gives us an initial potential energy of
. This
gives us an initial potential energy of 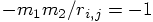 ,
since we are working with
,
since we are working with 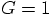 . Because of the virial theorem,
we know that the average kinetic energy has to be
. Because of the virial theorem,
we know that the average kinetic energy has to be 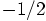 times
that of the average potential energy. In a circular binary, both kinetic
and potential energies remain constant, and equal to their initial values,
and therefore the total initial kinetic energy is
times
that of the average potential energy. In a circular binary, both kinetic
and potential energies remain constant, and equal to their initial values,
and therefore the total initial kinetic energy is 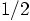 , in the
center-of-mass frame. This means that we need to give each star a kinetic
energy of
, in the
center-of-mass frame. This means that we need to give each star a kinetic
energy of 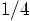 . Since each star has a mass of
. Since each star has a mass of 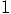 ,
the velocity
v of each star should be
,
the velocity
v of each star should be 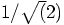 , in order to make
, in order to make
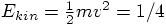 for that star.
for that star.
2
0
1
0.5 0
0 7.071067811865475e-01
1
-0.5 0
0 -7.071067811865475e-01
I'll use the same parameters for the fourth-order Runge-Kutta integrator,
in my N-body code:
|gravity> ruby rknbody1a_driver.rb < test2.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.5 , E_pot = -1 , E_tot = -0.5
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.5 , E_pot = -1 , E_tot = -0.5
E_tot - E_init = -6.22e-15
(E_tot - E_init) / E_init = 1.24e-14
2
9.9999999999900329e+00
1.0000000000000000e+00
-2.4843310663498000e-03 4.9999382806106440e-01
-7.0709805274678161e-01 -3.5133746874538431e-03
1.0000000000000000e+00
2.4843310663498000e-03 -4.9999382806106440e-01
7.0709805274678161e-01 3.5133746874538431e-03
3.4. A Variation
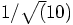 .
This means that the new velocity of each particle should become
.
This means that the new velocity of each particle should become
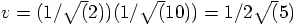 .
.
2
0
0.1
0.5 0
0 0.22360679774997896964
0.1
-0.5 0
0 -0.22360679774997896964
I'll use the same parameters for the fourth-order Runge-Kutta integrator,
in my N-body code:
|gravity> ruby rknbody1a_driver.rb < test3.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.05 , E_pot = -0.01 , E_tot = 0.04
E_tot - E_init = 0
(E_tot - E_init) / E_init = 0
at time t = 10, after 100000 steps :
E_kin = 0.05 , E_pot = -0.01 , E_tot = 0.04
E_tot - E_init = -2.64e-15
(E_tot - E_init) / E_init = -6.59e-14
2
9.9999999999900329e+00
1.0000000000000001e-01
-1.1897419599036606e-01 -4.8563889948034655e-01
2.1718431835122404e-01 -5.3206877960568291e-02
1.0000000000000001e-01
1.1897419599036606e-01 4.8563889948034655e-01
-2.1718431835122404e-01 5.3206877960568291e-02
3.5. Another Variation
2
0
1
0.5 0
0 0.5
1
-0.5 0
0 -0.5
Here goes:
|gravity> ruby rknbody1a_driver.rb < test4.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -1 , E_tot = -0.75
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.307 , E_pot = -1.06 , E_tot = -0.75
E_tot - E_init = -1.35e-14
(E_tot - E_init) / E_init = 1.81e-14
2
9.9999999999900329e+00
1.0000000000000000e+00
4.4625642676571020e-01 1.5717985834439904e-01
-3.3221408890524584e-01 4.4320400716535185e-01
1.0000000000000000e+00
-4.4625642676571020e-01 -1.5717985834439904e-01
3.3221408890524584e-01 -4.4320400716535185e-01
3.6. Two Variations
2
0
0.9
0.5 0
0 0.5
0.9
-0.5 0
0 -0.5
Try again:
|gravity> ruby rknbody1a_driver.rb < test5.in
dt = 0.0001
dt_dia = 10
dt_out = 10
dt_end = 10
method = rk4
at time t = 0, after 0 steps :
E_kin = 0.25 , E_pot = -0.81 , E_tot = -0.56
E_tot - E_init = 0
(E_tot - E_init) / E_init = -0
at time t = 10, after 100000 steps :
E_kin = 0.56 , E_pot = -1.09 , E_tot = -0.529
E_tot - E_init = 0.031
(E_tot - E_init) / E_init = -0.0554
2
9.9999999999900329e+00
9.0000000000000002e-01
2.1147553247493753e-01 -3.0575926734969655e-01
7.4020397769574453e-01 1.1195514589010475e-01
9.0000000000000002e-01
-2.1147553247493753e-01 3.0575926734969655e-01
-7.4020397769574453e-01 -1.1195514589010475e-01
Alice: Here we clearly have a problem, and a big one: terrible energy
conservation. So now we know that the problem does not depend on
having unequal masses, but it does seem to require both
non-circularity and masses that differ from unity.