1. Ruby Running Ruby
Alice: We've come a long way, starting with constant time steps,
then introducing adaptive time steps that were shared by all
particles, and finally switching to individual time steps. And we now
have a powerful and very modular version world3.rb that
contains a large choice of different integrators.
Bob: That is all nice and fine, but I'm getting ready to do some
real science. We have spent so much time on tool building, I would
like to see some actual experiments, leading to some new results.
Alice: Do you mean something like studying core collapse in star
clusters?
Bob: At some point, sure, but that would require quite a few other
tools that we don't have yet. At the very least, we would have to
introduce regularization methods for binary stars. We'll get to that
point, before too long, but frankly, right now I don't want to dive
into yet another round of tool building. Let's do something with what
we have.
Alice: Sounds reasonable. But we do have to work with our current
limitations. Which means: small N values, and no simulations which
involve long binary star integrations. That doesn't leave us that
much choice.
Bob: Putting it that way already suggests an interesting project.
Although we can't integrate binaries very accurately, for very long,
at least we can run each simulation until the first hard binary forms.
We can study how long it takes to form such a binary, on average.
Alice: That's a good idea! We can define the time for first binary
formation, as the typical time it takes to form the first binary.
Such a time will of course depend on the initial conditions, but we
may as well choose a Plummer model, to start from. After all, there
is a tradition in star cluster research, to base theoretical
investigations on Plummer's model.
Bob: So we can define
Alice: to make it precise, we'd better define what we mean with `typical':
do we mean the average, or the median, or some other measure?
Bob: I would say, let's start with the average, but it's a good idea
to record the median as well. In fact, we should record the outcome for
each individual experiment, so that we can later try different definitions.
Alice: So be it! How shall we get started?
Bob: The first step is to automatize the procedure of running a simulation.
If we want to establish the shape of the curve
Alice: Yes, that's the drawback of a Monte Carlo approach, that the accuracy
of an average over a sample increases only as the square root of the number of
elements in that sample. But we don't have any choice, if we want to measure
typical behaviors in a situation where each run will give a rather different
outcome. How do you envision setting up an automatic Ruby running tool?
Bob: The simplest way would be to just write a shell script. That is how
I have always orchestrated runs whenever I was involved in a simulation
project.
Alice: That is possible, but I must say, I'm not too thrilled with the idea
of having to use shell scripts. Some of the commands are rather arcane, and
then there are the subtle differences between a C shell and a Borne shell and
all those other UNIX shells that are in use. Can't we use Ruby itself to run
Ruby programs?
Bob: That should be possible, in principle. Let me have a look at the
manual. I remember seeing a way to execute shell commands from within Ruby.
Ah, here it is. Well, that's simple! You just enclose the UNIX command
within backquotes. Let's try it out. I'll open a file test0.rb.
What commands shall we start with?
Alice: How about measuring the convergence of an algorithm? We can run
an integration with three values for the accuracy parameter, and measure
the phase space distance between the first and second, and between the
second and third run. That will give us a sense of the rate of convergence.
We've done that before, by hand. Let's now do it in a Ruby script.
Bob: Okay, give me a few minutes, I'll try something out.
Alice: Did you succeed?
Bob: Yes, here it is. I'm using the shared time step code
nbody_sh1.rb. This now does the job:
Alice: Wow, how neat and careful, and with four well described options.
I'm impressed!
Bob: Well, now that we have built all this infrastructure, we may as well
use it. It will make it far easier to check later on what it was we
have been doing today. And besides, writing those options is easy:
I just copied them out of the original codes mkplummer.rb and
nbody_sh1.rb, and adjusted the wording slightly, to fit in
with the current purpose.
Alice: Yes, once you have the right tools in place, life does get a lot
easier. Let me see whether I can parse what you did. The first line after
the usual command line processing indeed is written between backquotes, so
the content between those backquotes will be sent to the shell. But why
the hash marks?
Bob: Those force an evaluation of what is between the parentheses.
If you would leave those out, and if you would just write:
Bob: I don't think it ignored clop.n. If it had done so, it
would produce the following result:
Bob: It seems that -n clop.n was converted to -n 0.
Alice: In any case, yes, I now see the need for the evaluations around
each option, in the shell command. In the next two lines you introduce
abbrevations in order to keep the following command lines to a reasonable
length.
Bob: I know you don't like to exceed 80 columns. Oh, those Fortran types!
Alice: Just a matter of keeping lines from folding in my standard editor
window. Okay, you then run the integrator for smaller and smaller
time step size parameters, decreasing the value in steps of ten. And finally
you determine phase space differences between pairs of output snapshots.
Bob: The tricky thing here was to put print in front of the last two lines.
At first, I left that out, and I did not get any output at all! It took me
a while to realize that giving a shell command in itself is not enough.
It would be carried out, of course, and the result would come back from the
shell to the program test0.rb. But then the result would only be
known internally within test0.rb. In order for us to see the result,
we have to specifically print it out.
Alice: Tricky! But of course, once you explain it, it makes sense.
It is all a matter of meta levels. There is the level of running the
Ruby programs nbody_sh1.rb and nbody_diff.rb and so
on, and there is the meta level of running test0.rb that in
turn is running those other Ruby programs. And in order to get the
results from the lower-level programs out, they have to be handed up
through the higher-level program.
Bob: Exactly. And before long, we will probably running programs that
run programs that run programs, adding more meta levels.
1.1. A Concrete Research Problem
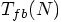as the typical time of
first binary formation, as a function of N, starting from a Plummer
model. I like that!
1.2. Toward Automatizing
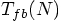, we
need to do many runs for each N value. We are talking about a type of
Monte Carlo experiment. In order to determine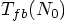 
,
for a particular value 
, to within an accuracy of, say,
ten percent, we need to carry out a hundred simulations, something I don't
plan to do by hand!
1.3. A First Test Script
1.4. Analyzing the Script
`kali mkplummer.rb -n clop.n`
our test code would send this line, literally as it is, to the shell.
Believe me, this is what I did first, of course, and here is what happened:
|gravity> kali mkplummer.rb -n clop.n
==> Plummer's Model Builder <==
Number of particles : N = 0
pseudorandom number seed given : 0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
actual seed used : 122151267828501582009483475313242352263
ACS
NBody
Array body
String story 2
actual seed used : 122151267828501582009483475313242352263
SCA
Alice: Ah, mkplummer.rb simply ignored clop.n and
gave you a Plummer model with zero particles. Not very interesting!
|gravity> kali mkplummer.rb
==> Plummer's Model Builder <==
Number of particles : N = 1
pseudorandom number seed given : 0
Screen Output Verbosity Level : verbosity = 1
ACS Output Verbosity Level : acs_verbosity = 1
Floating point precision : precision = 16
Incremental indentation : add_indent = 2
actual seed used : 90871704767965328566218331919121557706
ACS
NBody
Array body
Body body[0]
Fixnum body_id
0
Float mass
1.0000000000000000e+00
Vector pos
0.0000000000000000e+00 0.0000000000000000e+00 0.0000000000000000e+00
Vector vel
0.0000000000000000e+00 0.0000000000000000e+00 0.0000000000000000e+00
String story 2
actual seed used : 90871704767965328566218331919121557706
SCA
Alice: I see: one particle this time. A bit better, but still not what
we wanted.