3. The NBody Class
Alice: I think I understand now how the Body class works. Could you
also print out the whole NBody class?
Bob: Sure. It's not very long, about the same size as the Body class.
I keep being surprised at how compact Ruby code is.
Alice: We already talked about the generic case, with a call to
autonomous_step. Now I would like to see how the whole
thing starts up.
Bob: At the very bottom of the file, the evolve method is evoked
as follows:
The startup function makes sure that the acceleration and jerk are being
computed properly at the beginning of the integration. But in order to
do so, it first has to set the predicted positions and velocities
pred_pos and pred_vel to the right values, namely the
values of the initial positions and velocities.
In the Body class we saw the following generic order: 1) we predict
the positions of all particles, using predict_step; 2) we
compute the acceleration and jerk on one particle and set the next
time step value; 3) we step that particle forwards using correct_step.
We use the same order here, at startup, which occurs at the time
@time, the instance variable for the NBody class. This is
the time that has been read in from the initial snapshot; and if there
is no time listed in that input file, the default time @time = 0
is used default, since this is the time that has been assinged by the
NBody#initialize method in file nbody.rb.
For startup, step 1), prediction, is trivial: starting at time @time
we predict where all particles will be at time @time, in other words
we don't have to do anything; we just copy the position and velocity values
that were just read in.
Step 2), the calculation of acceleration and jerk and the next time step
value, can only be done after step 1) has been completed for all particles.
This is the reason that we need to different each loops in startup.
Step 3), correcting the positions and velocities, is not necessary at
startup: no particle has been moved, so there is nothing to correct.
Alice: Thanks, that's very clear. Then, after startup, we enter the
while loop in evolve, evoking autonomous_step for each next
particle that needs to be propagated. Let's have a look at how
find_next_particle is implemented.
Bob: Here we loop over all particles, to find the particle with the
earliest next sales date next_time. The method
find_next_particle then returns the body that has the smallest
next_time value.
Alice: So time is marching forward. When we enter
find_next_particle, the NBODY time @time has a certain
value. We then are given a body b which has a value b.next_time
for which we know that b.next_time > @time and we also know that
for all other bodies ob we have ob.next_time >= b.next_time.
Bob: Correct.
Alice: This means that in the interval between @time and
b.next_time there is nothing that needs to be done. Then we
set the NBody time @time equal to b.next_time, and
we push particle b forwards by one step.
Having done that, we again look for the next particle, through a new
call within evolve to find_next_particle. Perhaps the time
for the newly found particle is the same as that for the previous
particle, in which case @time doesn't change; perhaps it is
later, in which case @time is updated to the latest sales
date of the new particle.
Okay, I think I got it! I just had to reconstruct the steps for myself.
This is not a trivial algorithm!
Bob: As always, it is all pretty clear once you understand it clearly,
but I must admit, it took me quite a while to figure it out, the first
time I came across an individual time step code.
Alice: We're almost there. I just have to figure out now how the
particles are synchronized before you do an output, either a full
particle output in terms of a snapshot, at time t_out, or a
diagnostics output at time t_dia.
Let me put the need for synchronization in perspective. In the case
of our constant time step code nbody_cst1.rb, synchronization
was trivial: in typical usage, you specify output times that are multiples
of the prescribed time step. And if you were to set a time step to, say,
0.01 and an output time to an incommensurable time 1/3, then the code would
slightly overshoot, and give the output at time 0.34, instead of time
0.333333. We could have added an option to allow us to shrink the
last time step in such a case, to reach the value 1/3 exactly, at
least within double precision. However, there was no pressing reason
to do so.
In the case of our shared time step code nbody_sh1.rb, we did
build in such an option. Invoking it by default would let the code
overshoot, since in general the chance is virtually zero to get
commensurability between a prescribed output time and dynamically
adjusted time step values. However, by invoking the code with the
option nbody_sh1.rb --exact_time, we could force the code to
halt at the exact time desired. This was essential for us in order to
measure the phase space distances between different N-body systems
generated in the output of different runs.
Now in the case of our individual time step code nbody_ind1.rb,
we have no choice. We cannot afford the luxury of skipping synchronization,
since in that case we would get an output of a bunch of particles, all at
different times. We couldn't even compute the energy of sych a system!
And this is the reason that you synchronize, for every type of output.
Bob: Yes, that is the big picture. Note, however, that my insistence
on synchronization is not the only solution. I wanted to get
something coded up quickly, and I knew it was essential for measuring
energy conservation, so I implemented syncing by default. However, if
you just want to make a dump of the system, to allow future restarts,
there is no reason to insist on all the particles having their state
set at the same time.
Alice: Ah, yes, of course, I had forgotten that. Indeed, if you
do synchronize, you are guaranteed not to follow the same trajectory
when you restart from an earlier output. We showed this in the previous
volume, in the case of a shared time step code.
Well, what do you think, shouldn't we implement such a `ragged' output,
with the orbits of different particles extending in time to different
distances?
Bob: Ragged?
Alice: I'm trying to visualize what is going on. I can see a picture
in front of me, in spacetime, with each particle following a worldline,
where some worldlines are extended further than others, like a ragged
carpet where the different strands have different lengths.
3.1. Code Listing
3.2. Starting Up
: inccode:.nbody_ind1.rb-3
An N-body system is read in, and all that happens is a single call to
evolve, while the command line arguments are being passed along, just
as we already saw in the previous code.
3.3. Finding the Next Particle
3.4. Output
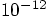 ? If we get too
close to machine accuracy, it may be more difficult to interpret our
results.
? If we get too
close to machine accuracy, it may be more difficult to interpret our
results.
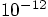 threshold too. Now
for individual time steps:
threshold too. Now
for individual time steps:
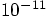 . That may not be so bad; there is no guarantee that
the phase space distance should give the same result as the energy error.
. That may not be so bad; there is no guarantee that
the phase space distance should give the same result as the energy error.