1. The Basic Idea
Alice: We now have a code for constant time steps, and one for variable
but shared time steps. It's time to bite the bullet, and start
working on a code where each particle will have its own individual
time step.
This will be quite complicated, but it is certainly necessary. When two
particles approach each other closely, we don't want to force all
other particles that are far away to take the same small time steps as
the closely approaching particles will take.
I've never coded up such a scheme, and I've never seen it in text
books on numerical integration either. It seems to be a special trick
that is used in astrophysics, in the stellar dynamics community.
I presume that you have some experience with . . . why are you smiling?
Bob: Yesterday, after we made such strides with our shared time step
code, I just couldn't stop. I've been hacking away the whole evening,
and I must admit, a good deal of the night. But I now have a working
individual time step version! It's right here under our fingertips,
in file nbody_ind1.rb.
Alice: So that's why you are smiling, you have every right to do so!
Bob: And I must admit, yes, I do have some experience. In no way could
I have come up with all the tricks of the trade in just one night. The
most tricky thing is to visualize the scheduling requirements. But why
talk about it abstractely if I can show you concretely what I did?
Alice: Please do!
Bob: First of all, I limited myself to the Hermite scheme.
Alice: Why? After you had derived all those nice integrators, why
not carry them over?
Bob: I can see that you don't have experience with individual time step
schemes. And in that light, it certainly is a fair question. The answer
is that not every algorithm comes with a predictor.
Alice: A predictor?
Bob: Yes. A predictor. Okay, lets start at the basics. If particles
have individual time steps, how do you think a single particle will
make its next step?
Alice: That will depend on the algorithm.
Bob: Let's say that you have a Runge-Kutta scheme. For definiteness,
let us take the second-order Runge-Kutta scheme rk2 that we have
been using.
Alice: Well, in that case it will first make a half-step, with a length
of
Bob: How will our particle take that step?
Alice: Is this a riddle?
Bob: No, I'm serious. How does the particle step forward?
Alice: How does the chicken cross the road. Well, of course, you take
the velocity and acceleration . . .
Bob: . . . How do you obtain the acceleration?
Alice: In the usual way, as the inverse square of the distance between
. . .
Bob: . . . How do you determine the distance?
Alice: You take the position of the other particle and . . .
Bob: . . . How do you know the position of the other particle?
Alice: You look it up! Will you never let me finish a sentence?
Bob: I just did. Now, how do you look it up?
Alice: You look at . . . ahaha! Now I get it. The other particle has
a different time step size, so it will have a position all right, but
a position that is valid for a different time than the time for which
the position of our particle is valid.
Bob: So we have to extrapolate the position of the other particle, to
predict where it will be by the time we need its position.
Alice: Hence the need for a predictor.
Bob: Exactly.
Alice: That is tricky indeed. How do you use a Runge-Kutta scheme to
provide a predictor?
Bob: The answer is: you don't. Or at least astrophysicists don't.
They tend to stick to a very small set of algorithms with known predictors.
Alice: But wait a minute. For a second order Runge-Kutta, it should not
be too hard to construct a predictor!
Bob: That may be, but I'm sure it's non-trivial already for a fourth-order
Runge-Kutta. And this is why you've never heard of a code for collisional
stellar dynamics that uses a Runge-Kutta.
Alice: Ah, is that the reason that people only use Hermite and multi-step
methods?
Bob: It's not the only reason, I think, but certainly one of the reasons.
Alice: Not a very good reason, for sure. Just the fact that something is
not so easy to do doesn't mean you shouldn't try! I'm happy to start with
your Hermite implementation, but I sure would like to try other ones as well.
Let's set ourselves a goal, to make a fourth-order Runge-Kutta integrator!
Bob: That's quite a challenge. In the almost half century that astronomers
have worked with individual time steps, I've never seen or heard about
a Runge-Kutta implementation. But why not? If we succeed, it would
mean that in at least one respect we would be ahead of the pack.
Alice: I'd love to see that! But okay, for now let's be content with
Hermite. Can you show me what you did?
Bob: Let me skip the start-up phase for now. Often in life, it is not
so easy to start at the beginning. Let's start in the middle instead.
Imagine that all of our particles have already taken at least one step.
Let me show you how which particle takes the next step.
Alice: How which what?
Bob: There are two questions here: at any given time we first have to
determine which particle needs to take a step, and then we have to
figure out how that step can be taken.
Alice: I'm all ears.
Bob: First a bit more background. In the past, the state of each
particle was characterized by a mass @mass, position
@pos, and velocity @vel, all given at a shared
system time @time, an instance variable of the class NBody.
In the case of individual time steps, each particle has its own time
@time, which is now an instance variable of the class Body.
In addition, since each body has its own time step, it has a predicted
time @next_time, again different for each body, which is the
time of completion of the next time step: @next_time - time is
by definition the indivdual time step of the particle.
The concept of a @next_time is an important one: it plays the
role of a latest sales date. If you go to the store to buy some cookies,
you can look at the box, and read the latest sales date. If that date is
in the past, you probably don't want to buy the cookies, since you can't
trust them to be fresh enough.
Alice: Though they won't go bad overnight, as soon as the latest sales
date has passed.
Bob: Neither will our particles lose predictability completely, after
@next_time, but still, it is a good measure of the time until
which we can predict the position of a particle. If another particle
needs to know the position of our particle at time t,, there is no
problem as long as t <= @next_time.
To sum up: each particle carries with it a predictor that allows it to
predict its own position during the interval [ @time, @next_time ].
Alice: If another particle asks for the position of our particle at time
t, within that interval, how does our particle communicate its predicted
position?
Bob: Through its instance variable @pred_pos. Here is the hand
shaking mechanism. First the other particle sends the time for which
it wants to get the information. If the time is outside the proper interval,
our particle will complain. If the time is within the interval, our
particle will oblige, and predict its position and velocity, and store
those values in the variables @pred_pos and @pred_vel.
The other particle can then read off the values, and determine the
acceleration and jerk exercised on itself by our particle.
Alice: Ah yes, jerk, we are dealing with a Hermite scheme, and therefore
you have to predict the velocity as well.
Bob: Indeed. For any other scheme that we have implemented so far,
it would suffice just to predict the position, since we would only
need the acceleration.
Alice: So our Body class now has four extra instance variables,
over and above what we had in the shared time stap class: time,
@next_time, @pred_pos, and @pred_vel.
Bob: Indeed.
1.1. The Need for a Predictor
1.2. Crossing the Road
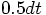 .
.
1.3. A Latest Sales Date