Bob: Oh, by the way, I decided to make a slight change in notation. So far, we have called our N-body class Nbody. However, it seems that in the Ruby community people have developed a clear convention to name all classes using the socalled MixedCase notation: each word is capitalized. Since in our case N and body are really different words, it would be much more consisten to call our N-body class NBody.

Alice: That's a really good idea. It is important to stick to the conventions that are used in a community. That will make it easier for others to read our code, and to jump right in, making their own additions. I guess this means that you will go back and change Nbody into NBody everywhere in the volumes that we've already written?

Bob: That would be a lot of work. Besides, it might confuse students and colleagues who have already downloaded some of our earlier volumes, if we were to suddenly change our notation, retroactively.

Alice: Again, you have a good point. Retrofitting what we have done, in order to make the past consistent with the present, is a dubious idea, I agree. Do you think it would be better not to do that, in general?

Bob: I think so. And since you like rules and abstractions, how about making this into a rule of ours: thou shalt not retrofit. Or in plain English: we will consider our work up till now read-only. We can add to it, but we will resist the temptation to clean it all up.

Alice: Perhaps in the future, if and when we make everything available as a book series, we could make a cleaning-up pass through the whole collection. But until that point, yes, I agree, let's just accumulate, rather than correct.

Bob: Of course, if we find plain mistakes, we should correct them, but other than that, we'll simply freeze each volume after we finish it.

Alice: The more I think about it, the more I realize that is the only way to go. After all, when we have 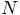previous volumes, the probability that we find some sort of minor inconsistency is at least proportional to 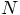. And if you take into account the way that inconsistencies may influence each other, you get something like compound interest, which was the way that the exponential function was first discovered! In the light of that, I guess the probability to be still consistent after 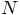volumes must be something like 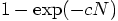for some constant c.

Even without taking into account compound effects, of changes triggering other changes, if one new volume gives rise to one incompatibility with each previous volume, we have 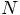incompatibility, which should then be repaired in each of the 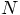previous volumes, giving rise to an amount of work of orde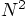r . For 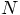new volumes, the work will scale as 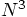. And that is using only the most optimistic assumption! Okay, I'm convinced.

Bob: Good! That will save us a lot of work.