19. Time Reversibility
Dan: I must agree, that is all very nice and clean. But let's get back
to the behavior of the two second-order algorithms that we have coded up
so far. Time symmetry is supposed to prevent a long-term drift. I'd like
to test that a bit more.
Let me take the modified Euler code, copying it from
euler_modified_vector.rb to
euler_modified_long_time.rb.
I will let the code run ten times longer, by changing the loop defining line
to:
Carol: I'm glad you're getting the hang of using long names. Thank you!
Dan: My pleasure. But see, I did still abbreviate a bit: I could have
left the word vector in, but that really would have made the
name too long, for my taste.
On a more important topic, I really don't like having different files lying
around that are almost the same, except for just one extra 0 in one line.
Carol: We'll have to do something about that. I had already been thinking
about introducing command line arguments.
Erica: What does that mean?
Carol: We really would like to specify the number of steps on the command
line, as an argument. It would be much better if we could take the program
euler_modified_vector.rb and run it for 10,000 steps, simply by
invoking it as
Dan: I would like that much better! Let's put that on our to-do list.
But for now, let me finish my long time behavior test. I'll write
leapfrog_long_time.rb, by modifying leapfrog.rb
in the same way, to take 10,000 steps:
Our expectation would be that modified Euler will completely screw up,
while the leapfrog will keep behaving relatively well. Let's see what
will happen!
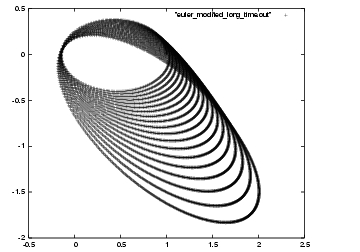
First I will make a picture of the long run for modified Euler,
in figure 39:
19.1. Long Time Behavior
|gravity> ruby euler_modified_vector.rb -n 10000
to indicate that now we want to take that many steps, or probably even
better
|gravity> ruby euler_modified_vector.rb -t 100
to indicate that we want to run for 100 time units.
|gravity> ruby euler_modified_long_time.rb > euler_modified_long_time.out
Next, I will make a picture of the long run for our leapfrog,
in figure 40:
|gravity> ruby leapfrog_long_time.rb > leapfrog_long_time.out
19.2. Discussing Time Symmetry
Carol: Your expectation was right, to some extent. Modified Euler is almost literally screwing up: the orbit gets wider and wider. In contrast, the leapfrog orbit keeps the same size, which is better for sure, but why does the orbit rotate?
Erica: Well, why not? A time symmetric code cannot spiral out, since such a motion would increase the size of the orbit. If an algorithm lets an orbit grow in one direction in time, it lets the orbit grow when applied to the other direction in time as well, as so it would not be time symmetric. However, if an orbit rotates clockwise in one direction in time, you might expect the orbit to rotate counter-clockwise in the other direction in time. So time reversal will just map a leftward rotation of the whole orbit figure into a rightward rotation, and similarly rightward into leftward
Dan: I don't get that. What's so different about expanding and rotating?
Erica: The key point is that we already have a sense of direction, in our elliptic Kepler orbit. Our star moves counter-clockwise along the ellipse, and we see that the leapfrog lets the whole ellipse slowly rotate clockwise. This means that if we let our star move in the other direction, clockwise, then the leapfrog would let the whole ellipse turn slowly in counter-clockwise direction. So the leapfrog algorithm would remain time symmetric: revolve within the orbit in one direction, and the whole orbit rotates; then revolve back into the other direction and the orbit shifts back again, until it reaches the original position.
However, during the course of one revolution, the orbit neither shrinks nor expands. Since there is no prefered direction, inwards or outwards, there is nothing for the leapfrog algorithm to capitalize on. It it were to make an error in one direction in time, say expanding the orbit, it would have to make the same error when going backward in time. So after moving forward and backward in time, during both moves the orbit would have expanded, and there is no way to get back to the original starting point. In other words, that would violate time symmetry.
Dan: Hmmmm. I guess. Well, let's first see how well this time
symmetry idea pans out in practice. Clearly,
nothing stops us from running the code backward.
After taking 10,000 steps forward, we can reverse the direction
by simply changing the sign of the time step value. I will do
that, and I will omit the print statement in the forward loop,
so that we only get to see the backward trajectory. If I would
print everything on top of each other, we probably wouldn't see
what was going on.
I will call the new code leapfrog_backward.rb, which is the
same as the old code leapfrog_long_time.rb, except that I
have replaced the original loop by the following two loops:
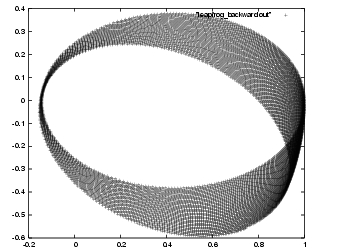
I will plot the backward trajectory in figure 41:
19.3. Testing Time Symmetry
|gravity> ruby leapfrog_backward.rb > leapfrog_backward.out
Carol: Figure 41 looks exactly the same as
figure 40!
Erica: Ah, yes, but that's precisely the point. The stars are retracing their steps so accurately, we can't see the difference!
Dan: Let's check how close the stars reach their point of departure, after their long travel:
|gravity> ruby leapfrog_backward.rb | tail -1 0.999999999999975 -1.06571782648723e-12 0.0 2.12594872261995e-12 0.500000000000013 0.0Wow, that's very close to the initial position and velocity, which we specified in our code to be:
r = [1, 0, 0].to_v
v = [0, 0.5, 0].to_v
Carol: But shouldn't the velocity have the opposite sign, now that
we're going backward?
Dan: No, I've gone back in time, using negative time steps, while
leaving everything else the same, including the sign of the velocity.
I could instead have reversed the direction of the velocity, while
leaving the time step the same. That would mean that time would keep
flowing forward, but the stars would move in the opposite direction,
from time
In this case, the final position and velocity are:
Erica: It is remarkable how close we come to the starting point.
And yet, it is not exactly the starting point.
Carol: The small deviations must be related to roundoff.
While the algorithm itself is strictly time symmetric, in the real
world of computing we typically work with double precision numbers
of 64 bits. This means that floating point numbers have a finite
precision, and that any calculation in floating point numbers will be
rounded off to the floating point number that is closest to the true
result. Since the rounding off process is not time symmetric, it will
introduce a slight time asymmetry.
Dan: Before we move on, I'd like to make sure that the rival of
the leapfrog, good old modified Euler, is really not time symmetric.
I will do the same as what we did for the leapfrog.
I will call the new code euler_modified_backward.rb, which is the
same as the old code euler_modified_long_time.rb, except that I
have again replaced the original loop by these two loops:
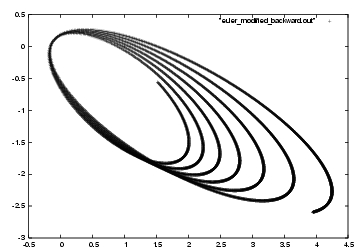
I will plot the backward trajectory in figure 42:
19.4. Two Ways to Go Backward
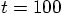 to
to 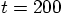 . Let me try that
too, why not, in leapfrog_onward.rb. This code is the same
as leapfrog_backward.rb, with the only difference being the
one line in between the two loops, which now reads:
. Let me try that
too, why not, in leapfrog_onward.rb. This code is the same
as leapfrog_backward.rb, with the only difference being the
one line in between the two loops, which now reads:
|gravity> ruby leapfrog_onward.rb | tail -1
0.999999999999975 -1.06571782648723e-12 0.0 -2.12594872261995e-12 -0.500000000000013 -0.0
Carol: Indeed, now the velocity is reversed, while reaching the
same point. Great, thanks!
19.5. Testing a Lack of Time Symmetry
|gravity> ruby euler_modified_backward.rb > euler_modified_backward.out
Carol: Figure 42 looks nothing like
figure 39. Even when you reverse the
direction of time, the orbit just continues to spiral out, like
it did before. You have now definitely established
that the modified Euler algorithm is not time symmetric!
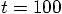 , with the
modified Euler algorithm, and step size
, with the
modified Euler algorithm, and step size 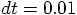 .
.
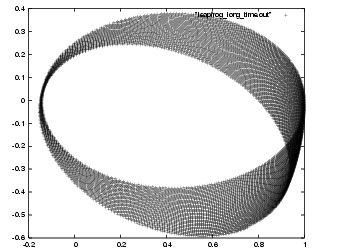
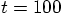 , with the
leapfrog algorithm, and step size
, with the
leapfrog algorithm, and step size 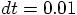 .
.
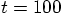 back to
back to 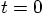 ,
and step size
,
and step size 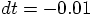 .
.
 back to
back to  ,
and step size
,
and step size  .
.