粒子法では現状どうだろうかというと今のところあんまり、、、というところ がありますが、FMM とかの実装を工夫すると実は行列乗算に書き換えられるか もしれません。例えば通常の FMM では一番計算量が多いのはいわゆる M2L の 部分であり、これは球面調和関数展開の係数に対してセル間の幾何学できまる 行列をかけることで処理できるはずです。行列乗算や行列ベクトル積が非常に 速い、という前提のもとでは FMM のコストのべき自体が変わってきます。

FMMが特に有効なのはクーロン力や重力のような 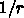ポテンシャルの場合 であるのはいうまでもありませんが、分子間力でも -6 乗、 -12 乗で、遠く ではもちろん展開可能です。但し、通常は規格化の係数に相互作用する原子の 半径の和がはいってきます。これはでも展開して半径の多項式にすればいいの かもしれません。

FMM の場合、単純な実装だと M2L で発生する変換行列は189個、対称性から (真面目に数えてませんが) 30個くらいまで減らせるはずです。 まともに行列乗算するか、例えば回転・変換・回転の組合せにして計算量を 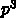(pは展開次数)にするかで行列の要素数、演算量も変わりますが、 例えば10次まで展開してまともにやったとして行列は1万要素、30個で30万語 なのでオンチップメモリに余裕で格納でき、これのロード・ストアは 計算時間の制約になりません。

そうすると、計算量のほとんどを行列乗算に押しつけることができるはずで、 FMM の計算で最も重いまま残るのが各粒子の位置での展開係数の評価、つまり ルジャンドル多項式の評価とすることができそうです。

というわけで、ちょっとまだ本当かどうかわからないですが粒子法にも 行列乗算専用回路は十分有効という気がしてきたので、 演算回路の構成と消費電力を少し考えてみます。

行列乗算回路といっても、ある程度プログラム可能にしておこうと思うと、単 純な構成は SIMD (MIMD でもいいですが私が設計して性能だせる気がしないの で)のプロセッサアレイの各 PE に小規模な行列乗算回路をつけることでしょ う。例えば、倍精度で 4x4 程度の行列乗算を、乗算器16個で実現する回路を 考えます。そうすると、これは4サイクルかかるので、行列の一方を使い回す とするとサイクル毎に4要素のベクトル1本を入力して1本を出力する回路にな ります。そうすると、自然な構成は、 4PE に1つこの回路をつけて、行列乗算 モードではフルに、通常の SIMD モードでは12個の演算器は殺して使う、とい うことになります。この構成で、論理回路と消費電力の大半を乗算器が喰う、 という構成にできると思われるので、これ以上、例えば8x8の乗算器にする、 という必要はないものと思います。

さて、この行列乗算回路で、単精度や半精度の演算をすることを考えます。 単精度だと 8x8 で、単精度乗算器が32個だと考えると2サイクルでベクトル1 本処理になります。回路をがんばって単精度演算器だと64個あるようにすると、 1サイクルでベクトル1本処理できてレジスタインターフェースとしては変わり ないことになります。 半精度も同様で、256個乗算器がある形にして 1サイクルでベクトル1本が処理できるようにつくりたいところです。

ちょっと楽観的ですが、この回路構成でPEの数当りの電力消費が GRAPE-X の 2倍程度でできたとすると、演算数は4倍になるので倍精度でチップの電力製造 が 60GF/W というあたり、単精度だと240、半精度だと 960 になるわけです。 まあ話半分としても 16FF+ の NVIDIA PASCAL で半精度公称 70 GF/W なわけ なので、2世代前のテクノロジーで1桁以上高い数値は実現できる、ということ になります。同じテクノロジーなら 50倍くらいですね。倍精度だと同じテク ノロジーでやっと10倍ですが、、、

50倍電力性能あげるのは、ムーアの法則があって10年、今後は永久に無理かも しれないわけで、まあそれなりに作る意味はあるかもということになりそうです。

Previous

ToC

Next