| Previous | ToC | Next |
今回は、階層メモリアーキテクチャでのレジスタ・メモ間バンド幅について 検討します。
例えば、メモリから何か読んできて、レジスタのどれかに足す、という時に、 必ずロード命令と加算命令が必要です。実行レイテンシを短くしようと思うと、 メモリからデータを読んできた時点でこれは次の加算命令に使えるデータだか らと判断して、レジスタへのストアと並行して加算命令を実行する、とか いった複雑な処理が必要ですし、そういうことを色々やると制御が複雑に なり、バグも発生することになりがちです。
最近のLSIチップでは小容量のレジスタファイ ルとある程度大きなメモリブロックとのサイクルタイムやアクセスタイムの 差はあまりなくなってきており、ハードウェアコストの観点からは ロード・ストアアーキテクチャは時代遅れになってきていると考えられます。
と、ここまでは前置きで、ここからが本題です。ここまで書いてきたように、 本来現在の半導体技術からみてもっとも適切なアーキテクチャではメモリとレ ジスタの間のバンド幅を気にする必要はないのですが、現在存在している、ワ イドSIMD だったりさらにスーパースカラー実行できる浮動小数点演算ユニッ トが複数あったりするアーキテクチャでは話はそう簡単ではありません。
例えば、実行ユニットが2個あるプロセッサコアの L1 キャッシュを考えてみ ます。4-way SIMD で、データ幅が 32バイト、キャッシュのラインサイズも 32バイトだとしてみましょう。
そうすると、サイクル・実行ユニットあたり1つロードまたはストアが実行で きる、とするだけで、L1 はリードまたはライトが2ライン並列にできないとい けないことになります。さらに、L2 との転送もできないといけません。L2 と の転送の B/F を例えば2にしたいとすると、L2 との転送も、サイクルあたり リードまたはライトが1ラインできないといけないことになり、結局L1 は少な くとも3ポート同時にアクセスできないといけないことになります。
こういったマルチポートメモリはメモリセルから設計すれば作れなくはないで すが、シングルポートメモリに比べて巨大で消費電力も大きなものになり、 消費電力増加、チップ面積増加の大きな要因になります。従って、アプリケー ション性能が極端に落ちない範囲で、ロード・ストアのバンド幅を下げて しまうことができれば、大きな性能向上につながると考えられます。
というわけで、まずは例のごとく密行列乗算について、原理的な限界を検討し ます。行列乗算を外積型で実行する場合、基本操作は BLAS の DAXPY です。 つまり、
a[i] += b*c[i]の形です。まずは原理的限界を検討するので、SIMDである、ということは考慮 しないで考えます。この形で、 a も c もメモリにあり、 a をメモリに戻す、 と考えると、加算1、乗算1に対して2ロード、1ストアでお話にならないわけで すが、 a のほうはレジスタにおいたまま、とすればc の1ロードだけですむことに なり、 a を例えば16回とか32回とか使い回せれば a のロード・ストアのコス トはかなり小さくなります。但し、 b のロードコストがみえてくるので、 それが十分小さくなるためには a を格納できるレジスタの語数がある程度 必要ということがわかります。
レジスタに a を格納できる語数が 
、繰り返し回数を 
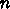とすると、
浮動小数点演算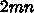 
回に対して c のロードが 
、
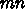a のロードが 
、 b のロード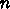が 
、
a のストアが 
で、メモリアクセスは
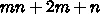と
なります。レジスタ語数にはコストがかかりますが繰り返し回数は
(原理的には)コストはかからないので、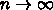 
の
極限を考えればよく、
浮動小数点演算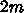 
回に対してメモリアクセスは
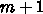となります。つまり、2演算に対して1ロード(加算器1つ、乗算器1
つに対してメモリからは1語ロードできるだけ)のアーキテクチャで、
レジスタ語数が 
の時極限的な実行効率は
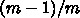になることがわかります。ここで、bに1語使うとし、
c の分は考えていません(ロード・ストアアーキテクチャなら1語は必要)。
2演算に対して1ロードは上で考えた仮想的なスーパースカラーマシン に相当しています。では、これをもっと減らせないか、が問題です。 基本演算が DAXPY ではもちろんこれ以上どうしようもないですが、 基本演算を小行列単位にすれば減らすことができます。 例えば、
a[i] += b*c[i]の各要素が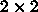
の行列であれば、a,c ともにメモリにあるとしても、
8ロード、4ストアに対して8乗算、8加算なのでロード・ストアに対する演算量
が行列単位でない時の倍になっている、言い換えると必要なロード・ストアの
バンド幅が半分になることがわかります。行列サイズを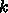 
として、
上と同様な解析をすると、
レジスタに a を格納できる語(行列数)数が 
、繰り返し回数を 
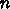とすると、
浮動小数点演算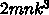 
回に対して c のロードが 
、
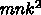a のロードが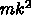 
、 b のロードが 
、
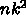a のストアが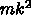 
で、メモリアクセスは
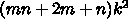と
なります。レジスタ語数にはコストがかかりますが繰り返し回数は
(原理的には)コストはかからないので、 
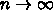の
極限を考えればよく、
浮動小数点演算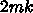 
回に対してメモリアクセスは
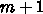となります。つまり、
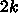演算に対して1ロード(加算器1つ、乗算器1
つに対してメモリからは1語ロードできるだけ)のアーキテクチャで、
レジスタ語数が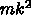 
の時極限的な実行効率は
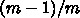になることがわかります。
ぎりぎりのメモリバンド幅で実行効率を例えば 90\% にしようとすると、
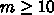が必要で、例えば 
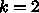なら40語必要となります。
これはあまり具合がよくないのですが、例えばSIMD 実行ユニットで
レジスタ1本が4語あれば10語でよいことがわかります。
逆に、ぎりぎりのメモリバンド幅にならないように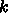 
のほうを大きくす
ることを考えます。
つまり、2演算に対して1ロード(加算器1つ、乗算器1
つに対してメモリからは1語ロードできるだけ)のアーキテクチャで、
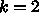とすると、a, b, c がそれぞれ(2x2行列)1つはいれば
実行効率が100% となります。これは実は内積型に書き換えたのと
同じです。
これから具体的にいえることは、例えば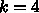 
のコードを書くことができ
れば、原理的にはレジスタは48語(4-way SIMD なら12語)あれば、L1のバンド
幅を通常必要な4ではなく2にしてもL1のレベルでは100%の実行効率を実現でき
る、ということです。もちろん、レイテンシとか色々あるので実効的に使える
レジスタの数はもっと減るかもしれなくて、少なくとも物理レジスタとしては
もうちょっと沢山必要かもしれませんが。
つまり、行列乗算だけを考えた時には、ワイドSIMDには、「レジスタの総語数が 増える」というメリットがあり、それを有効に使うことでレジスタ・メモリの 転送バンド幅を減らすことが可能になります。
行列乗算はそうかもしれないけどそんなの他に使い道ないのでは？という疑問
をもたれることと思いますが、例えば粒子系の相互作用計算なら、同様に
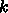個の粒子と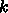 
個の粒子の相互作用を計算、とすればよいので
あまり問題はありません。但し、作用・反作用の効率的な利用には、
水平加算命令があったほうが、、、という話になります。
差分法はこんなうまい話はありませんが、レジスタに差分計算に必要な数メッ シュがのればある程度のデータの使い回しができ、演算密度を上げることは 可能と考えられます。
Haswell あたりではDGEMM の効率がさがっているようですが、ここまでの考察 からわかることは、これは WIDE SIMD の限界というよりは WIDE SIMD の利点 を有効利用できていないため、言い換えると実装のどこか(命令セットの問題 かソフトウェアの問題かは私は知りません)が阿呆なせいである、と いうことになると思います。
レジスタ・メモリ間の転送バンド幅を減らせる、ということは、上にみたよう にL1メモリのポート数を減らせるということであり、ひいては L2 にも影響が あるわけで電力性能に非常に大きなインパクトを持ちます。もちろん、レジス タレベルでデータ再利用が高い効率でできていないと効率がでない、すなわち、 レジスタ・ヒット率が高いコードでないと性能がでないわけですが、ワイド SIMDでは必然的にレジスタの容量が大きくなり、レジスタ・ヒット率を上げる ことが可能になるはず、ということです。
| Previous | ToC | Next |