1. いろいろなモデル計算 (2020/4/10)
コロナウイルス(SARS-CoV-2) の感染がどのように広がるかについては色々な ことがいわれています。が、その背景にあるモデルはほぼ同じで、 Kermack and McKendrick の SIR モデル A contribution to the mathematical theory of epidemics, 1927, Proceedings of the Royal Society A です。これについての牧野による解説は 岩波「科学」5月号掲載予定の原稿に書いた通りなので、まずはそちら を御覧いただければと思います。
基本的にはこのモデルを使っているにもかかわらず、どう対策をする必要があ るか、については色々な人が色々なことをいっていて、大きな幅があります。 ここでは、そのうち3つを取り上げて、どのような違いが生じているか、それ は何故か、どれが信用できるか判断できるか、というあたりを考えます。
考えるのは
- 西浦博北大教授によって「8割の接触削減が必要」として示されているグラ フの背景にあると思われるモデル
- 大橋順東大教授による「ほぼ全ての発症者が行動量を45%に下げたとしても わずか1%でも行動を変えない人がいると その効果は大きく損なわれる」という主張の根拠となるモデル
-
佐藤彰洋横浜市大教授による、東京では現在の 2% まで接触削減が必要、
という主張の根拠になっているモデル
西浦教授は厚労省
新型コロナウイルス対策本部クラスター対策班のメンバーでもあり、これまで
クラスター対策の有効性を主張してきていましたが、4/7 になって
「接触8割減で感染急減」との主張が報道されるようになりました。以下は
中日 新聞
からの引用です
1.1. 西浦博北大教授
北大教授試算「接触8割減で感染急減」 宣言の契機?首相が強い関心
(中略)
西浦教授は数理モデルと呼ばれる手法を用いて感染状況を推計する理論疫学
の専門家。
教授の試算では、外出を欧米に近い形で厳しく制限し、人と人の接触を八割
減らす対策を取れば、十日〜二週間後に感染者が一日数千人のピークに達して
も、その後に対策の効果が表れ、急速な減少に転じる。
どのようなモデルでなにを計算したのかがあまりきちんと説明されていないこ
ともあり、若干の混乱がありますが、以下のモデルで公開されているグラフを
ほぼ完全に再現できました。
規格化した方程式系
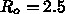
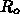 を 20% および 80% 減少させる
を 20% および 80% 減少させる
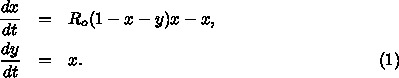
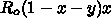 を、おそらく
を、おそらく 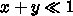 と近似してでてくる
と近似してでてくる
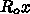 をプロットしています。ここで、
をプロットしています。ここで、  、
、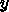 は全人口に対する
現在感染している人、感染から回復した人の割合です。
は全人口に対する
現在感染している人、感染から回復した人の割合です。
 は連続的に変化するのですが、
は連続的に変化するのですが、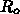 を突然変えるので
新規に発生する感染者の数はその分減るわけです。
そのあとは、
を突然変えるので
新規に発生する感染者の数はその分減るわけです。
そのあとは、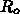 が1より小さくなれば、新規に発生する感染者数は指数
関数的に減少します。
が1より小さくなれば、新規に発生する感染者数は指数
関数的に減少します。
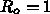 ) にした結果も示しています。
この場合にも減らないわけでではないのですが、減りかたは遅いことがわかり
ます。
) にした結果も示しています。
この場合にも減らないわけでではないのですが、減りかたは遅いことがわかり
ます。
「現在の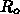 が2.5 であり」「SIRモデルを使い」「
が2.5 であり」「SIRモデルを使い」「 を80%減らせれば」こうなるよね、というグラフで、数学的にはおかしいとこ
ろはありません。
を80%減らせれば」こうなるよね、というグラフで、数学的にはおかしいとこ
ろはありません。
もちろん、実際にではある瞬間に 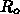 の原因となっている人と人の接触
を 80% 減らすことができたとしても、発生する陽性確定者や患者の数はこん
なに急には減りません。というのは、感染してから検査して陽性がでる、ある
いは発症するまでには何日かかかるからです。
の原因となっている人と人の接触
を 80% 減らすことができたとしても、発生する陽性確定者や患者の数はこん
なに急には減りません。というのは、感染してから検査して陽性がでる、ある
いは発症するまでには何日かかかるからです。
とはいえ、基本的な振舞いとしてこうなることを期待する、というのは大きな 問題はないように思われます。
大橋順東大教授の資料は
新型コロナウイルス感染症の 流行予測 正しく理解し、正しく怖がり、 適切な行動をとるために
です。
大橋氏は、SEIR モデルと言われる、少し複雑なモデルを使っています。これ
は、感染してから発症する(厳密には、人にうつすようになる)までに時間が
かかる、というモデルです。潜伏期がある、ということの簡単なモデルです。
方程式系は、この、感染したけどまだ人にうつさ
ない人の割合を e として
資料では、単純に
しかし、「科学」の記事でも述べたように、そもそも「
このことから、西浦氏のモデル計算と大橋氏のモデル計算に本質的な違いはな
いが、大橋氏の目標設定が55% と 西浦氏の 80% に比べて厳しくないのは、
「多数の死者を容認する」ことと少なくとも結果的には等価であることがわか
ります。
佐藤氏のモデルは4月7日の毎日新聞で紹介されました
これは、大橋氏のモデルをさらに複雑にした、遅延を微分要素ではなく
本当に時間遅れ(感染してからちょうど2週間後に発症)とし、
さらに確率的なゆらぎをいれたものです。確率的なゆらぎは
今回の解析にはほとんど意味がないのですが、
遅延モデルと、遅延の大きさには意味ががあります。
確率的なゆらぎを無視し、遅延をいれた方程式系は、以下のようになります。
4/16 追記
@ceptree 様から
SEIR epidemic model with delay
という論文があることを御教示いただきました。これの 1.3 式から通常の誕
生・死亡を除いたものが上の私が修正した方程式系になっています。
4/16 追記終わり
遅延は非線型項なので、大橋氏のものでやったような線型解析はやりにくいのですが、
できないわけではありません。e,x,y が1より十分小さいとすれば、この方程式系は単に
また、
このモデルでも
1.2. 大橋順東大教授
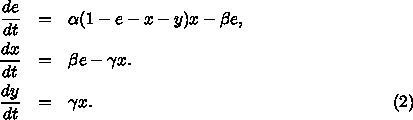
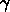 は1としてよくて、 e,x,y が小さいところでは
yの振舞いは e, x に関係ないの
で、その時のこの方程式の振舞いは行列
は1としてよくて、 e,x,y が小さいところでは
yの振舞いは e, x に関係ないの
で、その時のこの方程式の振舞いは行列

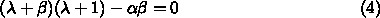
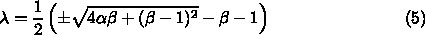
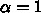 で0になることがわかります。なの
で、
で0になることがわかります。なの
で、 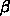 、つまり、潜伏期の長さに無関係に、
、つまり、潜伏期の長さに無関係に、 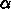 の値だけで
感染者が増えるかどうかは決まります。では
の値だけで
感染者が増えるかどうかは決まります。では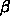 には意味がないか、と
いうと、これがあることによって固有値は常に
には意味がないか、と
いうと、これがあることによって固有値は常に 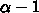 より小さくなります。つまり、
遅延があることによって、指数関数的な成長が、
より小さくなります。つまり、
遅延があることによって、指数関数的な成長が、
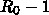 で決まるタイムスケールより遅いようにみえる、言い換えると
で決まるタイムスケールより遅いようにみえる、言い換えると
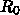 が小さいようにみえる、ということです。
が小さいようにみえる、ということです。
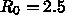 として、これを1程度にした場合を議論してい
ます。西浦氏の議論との最大の違いは、
として、これを1程度にした場合を議論してい
ます。西浦氏の議論との最大の違いは、
外出制限など各人の行動量(他人との接触頻度)をいかに40%(=1/Ro)に近づ
けるかが重要 (スライド24)
として、何故か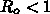 を目標としていないことです。このため、西浦氏資料と同じ
を目標としていないことです。このため、西浦氏資料と同じ
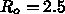 で議論しているのに、目標とする
で議論しているのに、目標とする
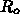 の減少の割合が80% と 55% で大きく違うことになります。
の減少の割合が80% と 55% で大きく違うことになります。
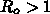 でしかも1に近い
ところ」は外出禁止等によってもっていくべき適切な目標ではありません。
これは、
でしかも1に近い
ところ」は外出禁止等によってもっていくべき適切な目標ではありません。
これは、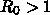 を維持すると膨大な死者がでるからです。
例えば、55%減らした、という時にはこのスライドの23ページにあるように、
全人口の概ね2割が最終的に感染します。死亡率を1%としても、
20万人が死亡することになります。これはあまりに膨大な数です。
を維持すると膨大な死者がでるからです。
例えば、55%減らした、という時にはこのスライドの23ページにあるように、
全人口の概ね2割が最終的に感染します。死亡率を1%としても、
20万人が死亡することになります。これはあまりに膨大な数です。
1.3. 佐藤彰洋横浜市大教授
福岡99.8%、東京98% 新規感染減に不可欠な「行動抑制率」 専門家が試算
感染拡大はどうしたら抑えられるのか、専門家によるシミュレーションが相
次いで出されている。ただ、緊急事態宣言の発令地域では人の行動を非常に
厳しく抑制しなければならず、現実的には極めて難しい。
佐藤彰洋・横浜市立大教授(データサイエンス)は発令地域を含む15都道府
県を対象に分析。自治体が発表する新規感染者数と、感染・発症後に回復す
る人の割合を基に、感染した状態の人数の推移を算出した。新規感染者が大
幅に増える時期より前の行動を「100%」とし、人と人との直接的な接触を
今後2週間で何%減らせば、長期間新規感染が確認されない状態に近づくか
目標値を示した。
その結果東京都の場合、公共交通機関の乗車時間と面会する人数を各個人が
98%減らす必要があった。
(後略)
この議論の根拠となるモデル計算は
都道府県ごとのシミュレーションによる検討です。
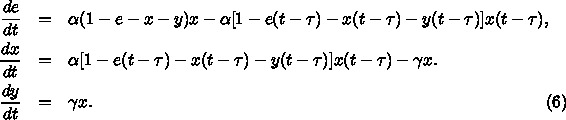
 つまり潜伏期の人の割合が明示的に
書かれていなくて、
つまり潜伏期の人の割合が明示的に
書かれていなくて、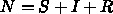 で
で 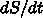 の第一項が
の第一項が
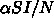 、つまり、規格化した変数で書くと
、つまり、規格化した変数で書くと
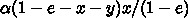 という少し不思議な形になっているようです。
以下の議論では e,x,y が1より十分小さい場合を考えるので、振舞いは変わら
ずここでの結論は同じです。
(最初のバージョンではここの記載に間違いがありました。 @ceptree 様に感謝します)
という少し不思議な形になっているようです。
以下の議論では e,x,y が1より十分小さい場合を考えるので、振舞いは変わら
ずここでの結論は同じです。
(最初のバージョンではここの記載に間違いがありました。 @ceptree 様に感謝します)

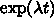 があるとして
があるとして

 を14日に固定しています。このため、
実際のこれまでの増加率をあらわすのに必要な
を14日に固定しています。このため、
実際のこれまでの増加率をあらわすのに必要な
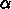 の値が1以上と極端に大きくなっています。
上の式を書換えると
の値が1以上と極端に大きくなっています。
上の式を書換えると

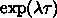 の値の分大きくなるからです。
の値の分大きくなるからです。
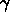 (佐藤氏の定式化では
(佐藤氏の定式化では 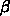 ) は、いくつかの都市で 0.01、
つまり、
他の人にうつさなくなるまで100日程度かかる、という値になっています。こ
れは、退院までの日数から推定したものと思いますが、おそらく日数を過大評
価、すなわち、
) は、いくつかの都市で 0.01、
つまり、
他の人にうつさなくなるまで100日程度かかる、という値になっています。こ
れは、退院までの日数から推定したものと思いますが、おそらく日数を過大評
価、すなわち、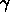 を過小評価しています。退院は、本当に確実に治っ
た、というところですが、人にうつす割合はもっと速くさがっているはずだからです。
を過小評価しています。退院は、本当に確実に治っ
た、というところですが、人にうつす割合はもっと速くさがっているはずだからです。
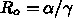 なので、
なので、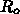 が100を超えるような極端な値にな
り、1%に落とす必要がある、という結論がでてくるわけです。
が100を超えるような極端な値にな
り、1%に落とす必要がある、という結論がでてくるわけです。
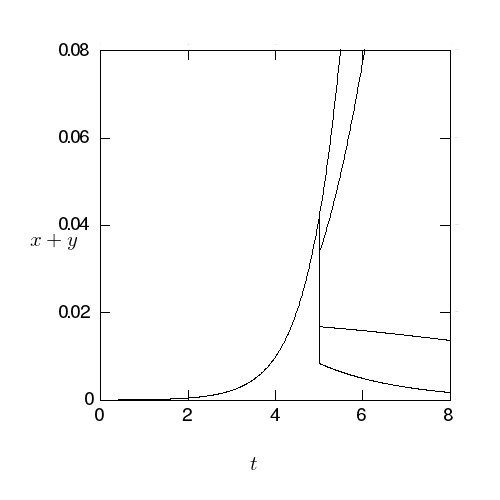
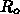 が変化しない場合の結果、
が変化しない場合の結果、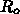 を20, 60, 80% 減少させた結果をしめ
す。
を20, 60, 80% 減少させた結果をしめ
す。
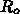 の減少率については、大橋氏はモ
デルパラメータが同じ西浦氏に比べて明らかに過小評価、佐藤氏はモデルその
ものが過大評価を与えるものになっていて、信頼できる結果とはいえないこと
がわかります。
の減少率については、大橋氏はモ
デルパラメータが同じ西浦氏に比べて明らかに過小評価、佐藤氏はモデルその
ものが過大評価を与えるものになっていて、信頼できる結果とはいえないこと
がわかります。
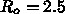 という仮定が正しい限りにおいては、単純
化したために現実との比較に注意は必要ですが、結果自体に大きな問題はない
ようにみえます。但し、
という仮定が正しい限りにおいては、単純
化したために現実との比較に注意は必要ですが、結果自体に大きな問題はない
ようにみえます。但し、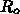 は中国での推定ではもっと大きいようでもあ
り、また、日本での現在までの検査体制で
は中国での推定ではもっと大きいようでもあ
り、また、日本での現在までの検査体制で
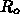 を正しく推定できるかどうかは原理的な問題を含んでいます。
従って、数理モデルとしては正しいものの、結果の「8割」を無条件に信頼で
きるとは
いえないのではないでしょうか。
を正しく推定できるかどうかは原理的な問題を含んでいます。
従って、数理モデルとしては正しいものの、結果の「8割」を無条件に信頼で
きるとは
いえないのではないでしょうか。